Beyond the blank page: Frequentist and Bayesian perspectives on risk prediction algorithms

Abstract

Risk prediction has long been a cornerstone of surgical oncology, enabling surgeons to anticipate complications, tailor perioperative care, and improve outcomes. With the rise of artificial intelligence, machine learning (ML) models are increasingly being applied to predict outcomes, highlighting the growing significance of data-driven methods for clinical decision-making. Currently, frequentist approaches dominate prediction models, including most ML algorithms; these rely exclusively on observed datasets and risk overlooking the cumulative value of prior clinical knowledge. In contrast, Bayesian reasoning formally integrates existing evidence with new data. In this letter, we examine the strengths of frequentist-based prediction models, discuss how Bayesian methods may improve predictive accuracy, and argue that combining both approaches offers a promising path toward more robust, interpretable, and clinically useful prediction tools in surgery. This integration can yield robust, interpretable, and clinically relevant tools that advance personalized surgical care.

Key Words: Gastric cancer; Bayes theorem; Artificial intelligence; Probability learning; Prediction algorithms; Risk

Core Tip: Risk prediction in surgical oncology is evolving beyond traditional scoring systems. Frequentist methods, widely used in machine learning, offer transparency and reproducibility but rely solely on observed data. Bayesian reasoning, by contrast, integrates prior clinical knowledge with new information, mirroring real-world decision-making. The integration of both frameworks promises more reliable, interpretable, and personalized prediction tools, advancing the future of surgical care.

TO THE EDITOR

A new era of risk prediction in surgical oncology

Risk prediction has always been central to surgical oncology. Anticipating which patients are more likely to experience complications allows surgeons to select patients for surgery, determine the optimal timing for surgery, optimize perioperative care, and ultimately improve outcomes. In recent years, new tools have emerged to refine this task. Machine learning (ML) and other artificial intelligence (AI) strategies are increasingly being applied to surgical prediction models, offering the promise of individualized estimates that can outperform traditional clinical scoring systems.

The recent study by An et al[1] represents a significant advance in this direction. In a retrospective cohort of more than 500 patients undergoing radical gastrectomy for gastric cancer, the authors developed predictive models for delayed wound healing, a complication with substantial clinical consequences. Using readily available clinical variables-sex, age, duration of abdominal drainage, and hematologic parameters-they compared the performance of three algorithms: Decision trees, support vector machines (SVMs), and logistic regression. Their results showed that decision trees achieved the best accuracy, recall, and F1 scores, underscoring both the feasibility and the potential of ML in surgical oncology.

Delayed wound healing is not merely a technical concern. It prolongs hospitalization, increases costs, predisposes to secondary infections, and delays the initiation of adjuvant therapies[2]. For patients with gastric cancer, where timely adjuvant treatment may determine survival, predictive models that identify high-risk patients are highly relevant.

The foundation: Learning from data with frequentist models

The study by An et al[1] follows the statistical tradition most widely applied in medical research: The frequentist framework. In this approach, inference is typically built on the logic of hypothesis testing, where the null hypothesis (H₀) is either rejected or accepted based on observed data. Within this paradigm, different ML algorithms can be applied to the same clinical question, each with distinct strategies for “learning” from data.

Logistic regression, one of the most established methods, models the probability of an outcome (such as delayed wound healing) as a function of several covariates. The resulting coefficients can be directly interpreted as odds ratios, which makes the model familiar to clinicians and easy to translate into risk scores. Its strength lies in transparency, but it does not capture complex nonlinear relationships unless interaction terms are explicitly introduced.

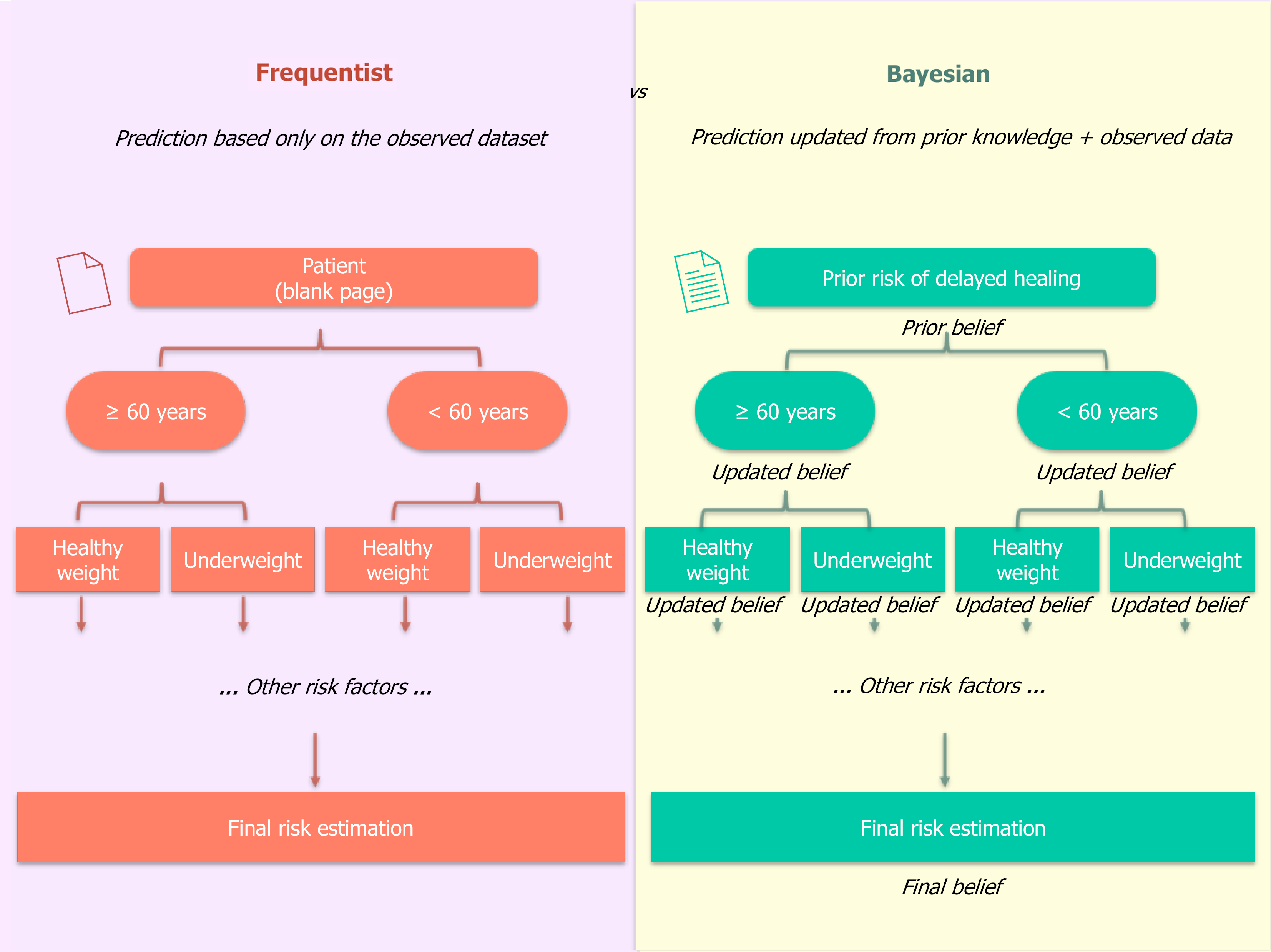
Decision trees take a different approach. Instead of modeling probabilities as a smooth function of predictors, they split the patient population into progressively smaller subgroups based on covariates. At each branch, the model asks a yes/no question. For example, it might first split patients based on age ≥ 60, then further split the older group based on body mass index (BMI) < 18.5, and so on, eventually reaching terminal "leaves" that assign a risk probability based on the proportion of events in that specific subgroup within the training data. This structure is highly interpretable, mirroring clinical decision pathways. However, it can be unstable, and the probabilities at each leaf are simple sample frequencies from the current dataset, starting from a "blank page" for each new patient.

SVMs, in contrast, are less intuitive but powerful in high-dimensional spaces. Rather than estimating probabilities, they focus on classification, drawing an optimal boundary (or hyperplane) that maximally separates patients with and without delayed healing. This can be especially useful when predictors are numerous or when relationships between them are not easily captured by traditional regression. However, because SVMs operate in a more abstract mathematical space, their predictions are more complex to interpret clinically.

Despite their methodological differences, these models share a common foundation: They rely exclusively on the observed dataset. They do not formally incorporate prior clinical knowledge, and they often treat covariates as independent contributors to risk. This makes them highly data-driven, but also potentially limited in contexts where prior biological plausibility or institutional experience has a significant impact beyond the data at hand.

The next frontier: Integrating knowledge with Bayesian reasoning

The Bayesian framework recognizes that each analysis builds upon what is already known, rather than assuming a blank page. Instead, it formally incorporates prior knowledge into the estimation process. Existing knowledge-whether derived from previous studies or institutional outcomes-is incorporated as a prior probability, which is then updated with new data to generate a posterior probability that reflects both past evidence and current observations. In this way, Bayesian inference reflects not only what is observed in the dataset but also the cumulative history of evidence, closely mirroring the reasoning process of surgeons at the bedside: The more information we accumulate-whether from a patient’s history, images, laboratory tests, or even clinical experience-the more refined and accurate our clinical judgment becomes. Bayesian models, therefore, generate probabilities that are both mathematically coherent and clinically aligned with how physicians reason: Integrating what is already known with what is newly observed.

On the mathematical point of view, Bayes’ theorem[2] states that the posterior probability of a hypothesis (H), given new data (D), is proportional to the likelihood of the data if the hypothesis were true, multiplied by the prior probability of the hypothesis, and normalized by the overall probability of the data (Figure 1).

Figure 1 Conceptual difference between frequentist and Bayesian probability.

Consider a patient undergoing radical gastrectomy for cancer. In a frequentist decision tree, being elderly may increase the observed probability of delayed healing (Figure 2). If the patient is also underweight (BMI < 18.5 kg/m²) with prolonged abdominal drainage, the estimated risk rises further, based solely on stratified frequencies in the dataset. In multivariable logistic regression, covariates are modeled simultaneously, as was done appropriately in the study by An et al[1]. However, like other frequentist models, SVMs and logistic regression rely exclusively on the observed dataset and do not formally integrate prior clinical knowledge. For example, sex and BMI are not independent variables: Men tend to have higher BMI values than women, which modifies how nutritional status influences surgical outcomes, while advanced age and impaired immune response often act synergistically to delay tissue repair[3,4]. In a Bayesian model, by contrast, we begin with a prior probability of delayed healing derived from prior evidence. This prior is then updated as we incorporate new information: Elderly status, sex, elevated preoperative white blood cell count, or high neutrophil levels. Each factor does not simply add to the risk; instead, prior knowledge about their interconnected impact informs how the posterior probability is shaped. In this way, Bayesian inference allows clinical intuition to be formally encoded into the prediction. In practice, this means that the statistical result is closer to the clinical question: A statistical point of view, this means that the statistical result is closer to the clinical question: Instead of a P value or rigid classification, the physician obtains the direct probability of benefit or adverse event for that specific patient[5].

Figure 2 Comparison between frequentist and Bayesian approaches to risk prediction. Frequentist models estimate risk based solely on observed data, while Bayesian models update prior knowledge with new evidence to refine the final probability.

Despite these advantages, Bayesian methods are not without significant limitations. The quality of their predictions depends heavily on the specification of prior distributions, which, if chosen poorly or based on limited evidence, may bias the results rather than refine them. Frequentist approaches are more straightforward to implement and easier to interpret. Their reliance solely on observed data, while sometimes restrictive, also ensures transparency and reproducibility without the need to justify prior assumptions.

Frequentist and Bayesian approaches: complementarity, not replacement

The study by An et al[1] is a valuable addition to the literature and an important step in bringing AI-driven prediction closer to surgical practice. By identifying relevant variables and demonstrating the feasibility of predictive modeling, the authors provide an essential foundation for more personalized perioperative care. Their work also invites a broader reflection on methodological choices in the field. Frequentist models remain the cornerstone of medical research due to their well-established transparency, reproducibility, and straightforward implementation. Bayesian approaches, however, offer a powerful complement by formally incorporating prior knowledge, a process that closely mirrors the way clinicians reason in practice.

The choice between models is context-dependent. In scenarios with sparse data-such as early-phase exploratory research or studies of rare conditions-Bayesian methods are particularly valuable, as they formally integrate prior evidence. This approach directly formalizes the implicit 'pre-test probability' that experienced surgical oncologists intuitively apply, derived from their individual experience, patient comorbidities, and institutional context. Conversely, for large multicenter datasets where reproducibility and simplicity are paramount, frequentist approaches often remain the standard. From a development perspective, each framework offers distinct advantages. The Frequentist framework, with its requirement for a fixed sample size and reliance on p-values for error control, provides a clear benchmark. Bayesian methodology, however, can enhance model stability, especially in small samples or high-dimensional data, by "borrowing strength" from prior information to avoid extreme estimates[6].

Given that both paradigms have merits, the focus should not be on choosing one over the other, but on their integration. Operationalizing this integration is key. Clinically, combining Bayesian and frequentist approaches empowers practitioners to select the most appropriate tool more effectively: For instance, using frequentist models for general population risk from large datasets and Bayesian models for highly individualized predictions where a specific clinical context is crucial. Methodologically, this integration can be achieved through sensitivity analyses that compare predictions across both frameworks. The work of Percival et al[7] demonstrated a prior selection technique that aligns Bayesian credible intervals with frequentist confidence intervals. This constructs a crucial bridge between the paradigms, allowing a Bayesian model's uncertainty estimates to be interpreted with frequentist coverage probabilities. Such a bridge gives developers and users greater confidence that the probabilities provided are both robust, statistically conservative, and clinically actionable.

The future of risk prediction in surgical oncology, therefore, does not hinge on a choice between frameworks, but on their rational combination. Integrating the rigor of frequentist statistics with the adaptability of Bayesian reasoning will yield predictive tools that are not only statistically sound but also clinically intuitive and actionable. This synergistic approach moves us closer to the ultimate goal of delivering truly individualized predictions to improve patient outcomes. In practice, this combination allows models to leverage prior knowledge for personalization while being rigorously tested against observed data. The result is a more informed clinical decision-making process, where estimated probabilities of outcomes are meaningful to both physicians and patients, effectively growing in a new era of predictive precision in surgical oncology.