Revised: December 8, 2010
Accepted: December 15, 2010
Published online: January 28, 2011
AIM: To present a content-based image retrieval (CBIR) system that supports the classification of breast tissue density and can be used in the processing chain to adapt parameters for lesion segmentation and classification.
METHODS: Breast density is characterized by image texture using singular value decomposition (SVD) and histograms. Pattern similarity is computed by a support vector machine (SVM) to separate the four BI-RADS tissue categories. The crucial number of remaining singular values is varied (SVD), and linear, radial, and polynomial kernels are investigated (SVM). The system is supported by a large reference database for training and evaluation. Experiments are based on 5-fold cross validation.
RESULTS: Adopted from DDSM, MIAS, LLNL, and RWTH datasets, the reference database is composed of over 10 000 various mammograms with unified and reliable ground truth. An average precision of 82.14% is obtained using 25 singular values (SVD), polynomial kernel and the one-against-one (SVM).
CONCLUSION: Breast density characterization using SVD allied with SVM for image retrieval enable the development of a CBIR system that can effectively aid radiologists in their diagnosis.
- Citation: de Oliveira JEE, Araújo AA, Deserno TM. Content-based image retrieval applied to BI-RADS tissue classification in screening mammography. World J Radiol 2011; 3(1): 24-31
- URL: https://www.wjgnet.com/1949-8470/full/v3/i1/24.htm
- DOI: https://dx.doi.org/10.4329/wjr.v3.i1.24
Breast cancer represents one of the main causes of death among women in occidental countries[1], and its early detection is the most effective way to reduce mortality with mammography posing as the best method of screening. Breast tissue density has been shown to be related to the risk of development of breast cancer[2], since dense breast tissue can hide lesions, causing the disease to be detected at later stages. As a result, there is also a decline in the sensitivity of mammography with increasing breast density. The Breast Imaging Reporting and Data System (BI-RADS)[3], developed by the American College of Radiology (ACR) (http://www.acr.org), provides a standardized density scale. BI-RADS defines density as (1) almost entirely fatty; (2) heterogeneously dense tissue; and (3) extremely dense tissue.
Besides visual evaluation and the report of breast density by radiologists, computer-aided diagnosis (CAD) and content-based image retrieval (CBIR) may assist the radiologist to improve the reliability of medical findings, and to decrease the number of breast biopsies from benign tissue[4-6]. CBIR aims at retrieving images from a database, which are relevant to a given query[7-9]. Information access is based on comparing visual attributes that are extracted from the image. The definition of a set of features (so-called feature vector or signature, which is capable of effectively describing each region of the image) and an appropriate similarity measure are the most complex tasks affecting all subsequent steps of a CBIR system[10].
An effective CAD or CBIR system, i.e. a system that provides diagnostic information of the image or a system that effectively presents similar images according to a certain pattern, must be evaluated using a large number of reference images with approved findings (ground truth). Nevertheless, published studies are usually based on a rather small set of data. For instance, Castella et al[11] developed a semi-automatic method in order to estimate the ACR breast density category using features extracted from 352 mammograms from Grangettes Hospital (http://www.grangettes.ch), Geneva, Switzerland. Sheshadri et al[12] used 60 mammograms of the Mammographic Image Analysis Society digital mammogram database (MIAS) (http://peipa.essex.ac.uk/ipa/pix/mias/) to characterize breast tissue density according to the BI-RADS categories. The mean, standard deviation, smoothness, third moment, uniformity, and entropy from the intensity histograms have been used to describe the tissue texture. Wang et al[13] used 195 mammograms from the Medical Center of Pittsburgh (http://www.upmc.com/Services/Radiology/Pages/default.aspx) in order to automatically evaluate breast density according to the BI-RADS categories. Bovis et al[14] proposed to increase breast cancer detection sensitivity through breast density classification using 377 mammograms taken from the Digital Database for Screening Mammography (DDSM) (http://marathon.csee.usf.edu/mammography/database.html), although DDSM provides about 10 000 images. Therefore, the reliability of classification rates published in these studies is ambiguous, and the smallness of the data hinders the generalization of results obtained.
Furthermore, the appropriate characterization of images, the storage and management of the large amount of image data produced by hospitals and medical centers are not straightforward issues to be jointly taken care of. Although large databases for mammography are publicly available[15], the problem of reference data requirement is manifold, and a sufficient number of appropriate cases for CAD and CBIR development and evaluation is needed.
From a clinical point of view, CBIR systems based on breast density can guide radiologists in the detection of a lesion and its classification. Moreover, from a technical point of view, this system is the first step, and a very important one, for the development of a CAD system. Based on the Image Retrieval in Medical Applications (IRMA) (http://irma-project.org) framework[16], we aimed to define a unified database structure and coding scheme for mammography that is associated with diagnostic information, and use this reference to develop and evaluate a CBIR system called MammoSVx, where singular value decomposition (SVD) and a support vector machine (SVM) are used for breast density characterization and retrieval, respectively. This article will contribute to a reliable and large reference database, and the combination and parameterization of SVD and SVM for automatic breast density classification.
The MammoSVx system was developed in several stages. In the following, we describe the composition of the reference database, which is used to respond to user queries. We also describe the feature extraction and selection process using SVD and the similarity measure based on the SVM. As part of our methodology, we describe the implementation of the system, as well as the design of the evaluation experiments.
The IRMA project aims to develop and implement high-level methods for CBIR with prototypal application for medico-diagnostic tasks on radiological image archives[16]. The database for mammograms integrated to the IRMA project was developed based on the union of the DDSM, MIAS, the Lawrence Livermore National Laboratory (LLNL), and routine images from the university hospital of Rheinisch-Westfälische Technische Hochschule (RWTH) Aachen University, Aachen, Germany[15].
The DDSM database[17] officially contains 2,479 studies (695 normal, 870 benign, and 914 cancerous cases). Each study includes two images of each breast, acquired in craniocaudal (CC) and mediolateral (ML) views that have been scanned from the film-based sources by four different scanners with a resolution between 50 and 42 microns, providing a total of 9916 radiographs. Since image coding was originally proprietary, they had to be converted to a standard file format with special software: the C source code provided at the DDSM web page needed extensions to cope with endianness, palettes, and others[15]. For all cases, ground truth is provided in additional ACSII text files including the BI-RADS tissue type classification and type as well as resolution of the scanner used to digitize the film-based mammograms.
The MIAS database[18] contains only 322 mammograms, all of which were acquired in the ML view. Initially scanned from film with a resolution of 50 microns, all images were reduced to 200 microns and clipped/padded so that they fit into a 1024 × 1024 bounding box. The image files are available in the portable network graphics (PNG) format and annotated with the following details: a database reference number indicating left and right breast, character of background tissue, pathology, class of lesion present and coordinates as well as size of these lesions.
The LLNL database[19] contains a total of 197 mammograms that have been digitized at 35 microns per pixel. The images are stored in the image cytometry standard (ICS) format and had to be converted to a standard file format with a program provided as source code. For 190 images, there is a plain text file containing patient status, biopsy results and ground truth comments.
In order to evaluate the extensibility of mammogram reference resources, 170 cases were extracted arbitrarily from the picture archiving and communication system (PACS) at the Department of Diagnostic Radiology, University Hospital, RWTH Aachen University, Aachen, Germany. These images were acquired digitally using a General Electric Senographe operating with low beam energy about 26 to 32 kV and with a phosphor storage system from Fuji/Philips capable of recording 7 lp/mm (approx 70 microns). The cassette was read using a Philips PCR Eleva CosimaX. Where available, a free text diagnosis in German describing the breast examination, pathology, type of tissue and lesion was included along with the digital imaging and communications in medicine (DICOM) files.
To uniformly integrate all data into the IRMA system, the IRMA code[20] was extended for mammography, and based on the meta-information available with all the databases, all images were coded consistently according to the mono-hierarchical, multi-axial IRMA ontology[15]. In particular, there are four axes, each having three to four hierarchical positions, which describe: (1) technique: The imaging modality axis of the coding scheme is used to differ direct digital and secondarily digitized imaging and their resolution; (2) direction: The body orientation axis captures the CC and ML views; (3) anatomy: The body region examined axis holds information on the left and right breast; and (4) biosystem: The biological system examined provides three positions that code the tissue density according to the ACR classes, the tumor staging according to BI-RADS[3], and the type of lesion, i.e. micro or macro calcification, speckled or circumscribed masses, architectural distortions, and asymmetry.
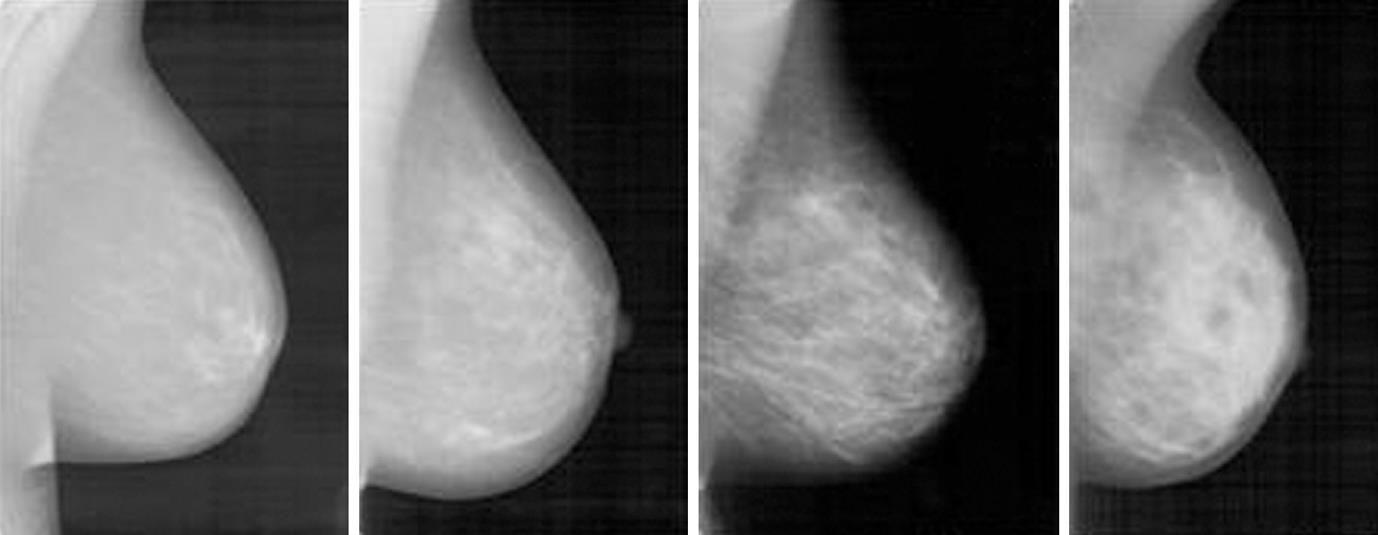
In machine vision, an image is represented numerically by a so-called feature vector (also referred to as signature), preferentially at a low-dimensional space in which the most relevant visual aspects are emphasized[21,22]. Visually, breasts of fatty and dense tissues differ through gray level intensities (Figure 1). Since texture contains information about the spatial distribution of gray levels and variations in brightness, its use for breast density assessment becomes appropriate[23]. However, the high dimensionality of a feature vector that represents texture attributes limits its computational efficiency, so it is desirable to choose a technique that combines the representation of texture with the reduction of dimensionality, in such a way as to make the retrieval algorithm more effective and computationally treatable.
SVD may satisfy these requirements representing the structure of the original data on a new basis in which the variables are ordered from the largest to the smallest degree of explained variation[24,25]. Wang et al[26] proposed a method of classification based on neural networks, in which the features used are the singular values of face images. For face photography recognition, the relevant technical properties of SVD are (1) stability (if a small disturbance is inserted in the image, the singular values alter only slightly); (2) algebraic properties, and; and (3) invariance of an image by the singular values.
Singular values represent important attributes of a matrix. As images can be observed as matrices, the singular values can serve as important features for evaluation of similarity. Also aiming to reduce the dimensionality and characterizing images in a medical CBIR system, Chen et al[27] applied SVD to represent color images of the stomach. SVD was performed on the color histograms to form a new feature vector. Concluding their study, the authors indicated the need for further studies to determine the optimal parameterization.
In general, let A be an m × n signature representing an image. Then, SVD is expressed as: A = UWVT (1). where U and V are orthogonal matrices, W = diag(λ1, λ2, ¡ , λk) and is the matrix of singular values of A with λ1≥λ2≥¡≥λk≥ 0 and k is the rank of A. For purposes of dimensionality reduction, suppose that matrix Uk of size m × k is composed of the first k leftmost singular vectors of U, matrix Vk of size n × k is composed of the first k rightmost singular vectors of V and the diagonal matrix Wk of size k × k is composed of the k singular values. Matrix Ak is defined as follows: Ak = UkWkVTk (2). The parameter k is crucial[27]. The smaller the value of k, the less storage and processing load is required, but if k is too small, important visual information is disregarded by the signature and retrieval results will become worse. In our study, k is determined by systematic experiments (see Experiments).
The support vector machine (SVM) method was initially developed to solve binary classification problems[28]. It guides the construction of classifiers with a good degree of generalization[29], i.e. with the ability of correctly predicting the class of a sample that was not used in the learning process. The use of SVM was extended to CBIR systems[30], where the similarity between images is measured by the relevance of an image to a particular query[31]. For instance, Yang et al[32] have used SVM specifically for CBIR of mammograms. However, SVM requires adjustments when applied to more than two classes, such as the four BI-RADS codes used for breast density classification.
Machine learning techniques may employ an inference principle called induction. The general conclusions are obtained from a particular set of examples[22]. In supervised learning, an external agent is used to indicate the desired answers to the entry patterns. The classifier is trained with a broad set of labeled data. Given a set of labeled examples as (xi,yi), where xi represents an example and yi denotes its label, one should be able to produce a classifier that can precisely predict the label of the new data. This induction process of a classifier from a sample of data is called training. The obtained classifier may also be seen as a function f that receives a dataset x and associated labels y. The labels or classes represent the phenomenon of interest on which one wants to make predictions. The labels can assume discrete values 1, ¡, p. A classification problem with p = 2 is called binary.
For a binary classification, SVM can be described as follows: given two classes and a set of points that belong to these classes, the SVM classifier determines the hyperplane in the feature space that separates the points in order to place the highest number of points of the same class on the same side, while maximizing the distance of each class to that hyperplane. The hyperplane is determined by a subset of items from the two classes, called support vectors. In most cases, however, the data set cannot be precisely separated by a hyperplane, so a kernel function is used instead. It receives two points xi and xj from the input space and computes the product between these data in the feature space. The most commonly used kernels are polynomial and Gaussian, in which the parameters must be empirically adjusted.
For more than two classes, this problem turns into a multi-class problem[33,34], which is the case of the MammoSVx system that works with four classes corresponding to the four BI-RADS categories for breast density.
There are two basic approaches for a multi-class application: (1) one-against-all: A SVM is built for each class through the discrimination of this class against the remaining classes. Successively, i.e. class by class, the decision is made. Let C denote the number of classes (here, C = 4). Then, the number of SVMs used is M = C-1. Hence, the MammoSVx system yields M = 3. Test data x is classified using a decision strategy, i.e. the class with the maximum value of the discriminant function f (x) is assigned to that data. All the n training examples are used to construct the SVM for one class. The SVM for one class p is built using the set of training data (x) and the desired outputs (y); (2) one-against-one: A SVM is built for a pair of classes through its training in the discrimination of two classes. In this way, the number of SVMs used in the method is M = (C-1)(C-2)/2 = 3. Here, one SVM for a pair of classes (p,m) is built using training examples belonging to only these two classes. This approach is a kind of generalization of the binary classification to more than two classes. Advantageously, all training examples are used at the same time[33].
With respect to the four BI-RADS tissue classes, both methods require three SVMs. In order to optimize the training phase providing all the data, we apply the one-against-one method to separate the four BI-RADS categories, two by two, for all experiments.
The MammoSVx system was implemented using MatLab (Matrix Laboratory), using the image processing and symbolic math toolboxes, and the LSSVM library[35]. It was executed on an Intel Core 2 Duo 2GHz processor with 3GB of RAM under the Microsoft Windows operating system.
The IRMA system is implemented in C and operated on a common Linux/Unix system. The PostgreSQL database is used to manage image, feature, and feature transform data[36]. Web-based access is provided by PHP hypertext preprocessor and the Smarty template engine (http://www.smarty.net)[37].
The methodologies were fused to MammoSVx (Figure 2). To remove noise, examination labels and other annotations from all images, regions of interest (ROI) were extracted. In a first step, a standardized image size was obtained shrinking all mammograms into a format of 1024 ×Z pixels, where Z varies according to the aspect ratios of the radiographs between 300 and 800 pixels. In this step, linear interpolation is applied. In the resulting scale, the size of the ROI that was extracted automatically was set to 300 × 300 pixels, which ensures the ROI contains tissue pattern only. Thereafter, the textural features were extracted using the SVD method, and compared to the features in the IRMA reference database using the SVM method.
Selection of image data: The IRMA database was merged from data of different sources and provides a reliable base for parameterization and evaluation of CBIR and CAD applications. Using the IRMA code, groups of reference images can be easily formed. As a result, the data used in the experiments were uniformly mixed from directly digital acquired and secondarily digitized mammograms of the left or right breast in CC or ML views with and without pathological alteration. However, the frequency of occurrence of tissue type in the IRMA database differs. To ensure an equal distribution for classification experiments, all images from the least frequent BI-RADS class are used, and the same amount is taken arbitrarily from the other classes.
Extraction of features: SVD was performed for all selected mammograms. The first k singular values were kept for the composition of the feature vector. The values for k used in the experiments were 25, 50, 100, 150 and 200. These values were chosen empirically in accordance with Elden and Andrews[25,38]. Optionally, SVD features were combined with the gray level histogram, as histograms have been successfully used in previous work[12,13,39]. In addition, we analyze the impact of the gray level histograms using this information solely for retrieval.
Evaluation of MammoSVx for CBIR: The CBIR task keeps the physician in the loop. Usually, the user presents an image, and the system offers a set of, for instance, ten responses, visually displayed to the physician, who can select appropriate information from the responses, or refine the query.
For the evaluation of the CBIR system, measures of precision and recall were obtained based on the top 10 retrieved images. Precision is the ratio of the number of relevant images retrieved to the total number of irrelevant and relevant images, whereas recall is the ratio of the number of relevant images retrieved to the total number of relevant images in the database[40]. Both measures are usually expressed as a percentage. We apply 5-fold cross validation and variance analysis (ANOVA) to obtain the best configuration of MammoSVx.
Evaluation of MammoSVx as a classifier: Furthermore, one can think of using the MammoSVx system as an automatic classifier. In this setting, the physician is excluded from the loop, and the system is used for automatic decision making. There are several ways of combining the ground truth of a set of retrieved images and forming a decision. The easiest, but usually not the best way, is to return only one image, and simply decide whether it is from the correct class or not. In doing so, the obtained results can be best compared with others.
Hence, this evaluation was performed measuring the accuracy, which is the percentage of correctly classified images of a certain class over the ground truth of the total mammograms in that class. For this experiment, we apply 10-fold cross validation.
Based on international standards such as ACR and BI-RADS, we provided a scheme to integrate available mammogram databases using a standardized description of imaging modality and resolution, orientation and view, left and right position of the breast, tissue type, tumor staging and lesion description. Integrating different resources that are freely available in the Internet, our database currently holds 10 509 images from 232 different code classes.
BI-RADS tissue class II was found to be most common with about 4000 entries, and BI-RADS class I was at least represented with only 1256 images. According to the protocol defined in the previous section, 1256 radiographs were randomly selected from all the groups yielding a total of 5024 mammograms.
Table 1 shows the resulting parameterization of the SVM with polynomial, radial, and linear kernels. Depending on the kernel, k = 25, k = 100, and k = 200 performed best, respectively. Therefore, the polynomial SVM kernel was superior since it needed the least number of data. Table 2 shows the overall results. In general, the combination of SVD and gray level histogram outperformed SVD and histogram feature extraction.
| Parameters | Polynomial kernel | Radial kernel |
| Cost (C) | 10 | 1 |
| Gamma (g) | 0.00022 | 0.0055 |
| Epsilon (e) | 0.1 | 0.1 |
| Degree | 2 | - |
| k | Feature | Average precision (mean ± SD, %) | Trace of Ak | ||
| Polynomial | Radial | Linear | |||
| 25 | SVD | 79.42 ± 0.44 | 68.92 ± 0.05 | 75.36 ± 0.10 | 23 |
| SVD + histogram | 82.14 ± 0.30 | 70.48 ± 0.12 | 75.66 ± 0.01 | ||
| 50 | SVD | 76.61 ± 0.40 | 71.00 ± 0.09 | 75.12 ± 0.07 | 24 |
| SVD + histogram | 76.72 ± 0.50 | 71.47 ± 0.16 | 76.26 ± 0.04 | ||
| 100 | SVD | 77.91 ± 0.15 | 69.23 ± 0.16 | 75.32 ± 0.06 | 24 |
| SVD + histogram | 78.31 ± 0.14 | 71.75 ± 0.04 | 75.70 ± 0.18 | ||
| 150 | SVD | 76.85 ± 0.16 | 71.52 ± 0.06 | 74.41 ± 0.14 | 25 |
| SVD + histogram | 76.47 ± 0.20 | 68.76 ± 0.17 | 76.44 ± 0.16 | ||
| 200 | SVD | 75.69 ± 0.16 | 71.57 ± 0.06 | 74.80 ± 0.08 | 26 |
| SVD + histogram | 76.67 ± 0.23 | 70.87 ± 0.16 | 76.87 ± 0.04 | ||
| Histogram only | 50.00 | 50.00 | 67.80 | ||
The best average precision of 82.14%, 71.75%, and 76.87% was obtained using the polynomial, radial, and linear kernel functions, respectively (Table 2). The ANOVA variance analysis yielded statistical significance. In order to verify the number of singular values that really represent breast density, the trace of the matrix Ak of singular values was examined. The last column in Table 2 shows the average amount of variables that are represented by the k singular values. The diagonal matrix has k singular values that are significantly larger than the others, and the zero singular values usually appear as small numbers. For all different values of k, only 24 singular values really represented breast density, and so the other values could be considered irrelevant. In conclusion, k = 25 appropriately represented breast texture in a lower-dimensional space with maximized computational savings, and the polynomial kernel significantly outperformed the other configurations.
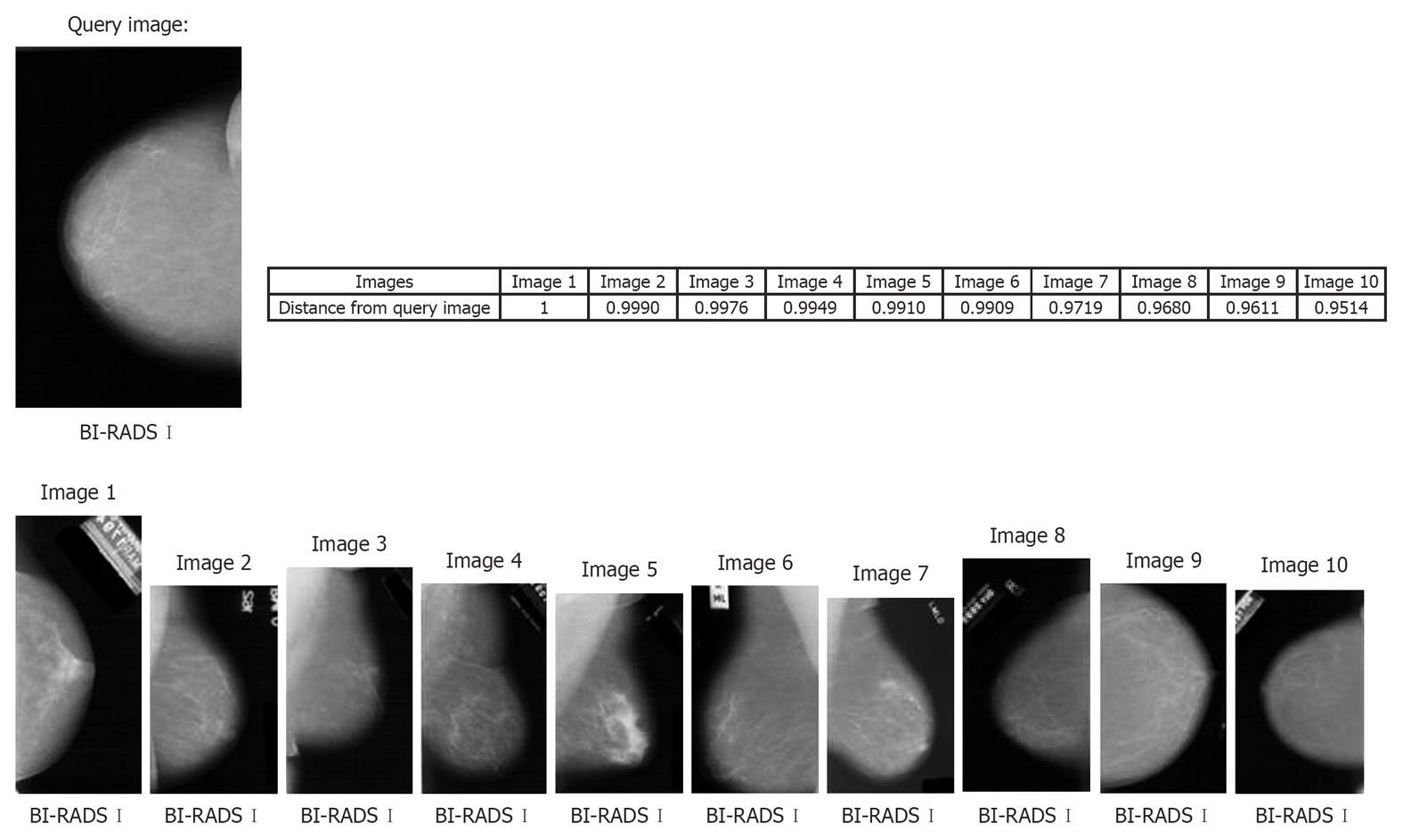
Figure 3 represents an example of the MamoSVx system, with a query image of BI-RADS category I for breast density. All the top ten retrieved images are from the same category of breast density of the query image. In this experiment, the system was not designed to differentiate the projection (CC or MLO) as only a ROI was selected for characterization, which does not consider the pectoral muscle (signature of the MLO projection). Also, the distance of these retrieved images to the query image is presented, where images with distance values near 1.0 are closer to the query image. Time of retrieval was 3.85 s.
Considering the classification experiment, an average accuracy rate of 76.4% was obtained.
We have presented a system design for CBIR for breast tissue density classification, which can be used directly to assist radiologists or as a preprocessing stage in CAD applications for lesion detection and tumor staging.
The evaluation of MammoSVx was based on a large database merged from a variety of sources, which supports the generalization of the experimental results. Furthermore, we were able to improve previously published results. For instance, Bovis and Singh[14] reported an average recognition rate of 71.4%, calculated on 377 images only, which is clearly below the corresponding finding in our experiment (76.4% obtained from 5,024 mammograms). This improvement was obtained by combining SVD with the gray scale histogram distribution. In other words, the chosen signature characterized breast density well. Furthermore, the small standard deviations obtained within the cross-over design (Table 2) indicate that our reference database was of sufficient size for the given problem.
An important characteristic of the MammoSVx CBIR system is the use of a priori breast density classification, as all the images contained in the IRMA database have their ground truth already set by an experienced radiologist. This supports the physician visually, as can be seen in Figure 3. Although radiologists might look further for breast lesions such as masses and calcifications in mammograms, a CBIR system for mammograms should include all possibilities. Therefore, MammoSVx may form the first stage of a CAD system, as breast density plays an important role in the diagnostic process.
Future work may focus on tests with more images and the combination of breast density, view and lesion as a pattern for retrieval. In addition, a weight combination of features should be tested in an attempt to avoid non-relevant images in the results.
Systems assisting radiologists in lesion detection and classification, or just presenting similar images to a sketched query are of great importance in clinical practice. They impact case-based reasoning, evidence-based medicine, and advanced blended learning techniques.
In screening mammography, the compilation of a large data collection with reliable ground truth is important to compile reliable systems for computer-aided diagnosis. Automatic detection of BI-RADS categories for breast tissue has not yet been solved, although several works on this topic has been published.
We provide a content-based image retrieval approach that relies on a large compilation of ground truth data in mammography. For computer-assisted diagnosis, breast tissue patterns are represented using a few singular values and a support vector machine for classification.
The Image Retrieval in Medical Applications framework provides server and client components to interface computer-aided diagnosis in routine clinical practice. A sample application is provided.
The topic is well presented and the article is reasonable. Some corrections need to be made, especially in the experimental section to improve the clarity.
Peer reviewers: Ragab Hani Donkol, Professor, Radiology Department, Aseer Central Hospital, 34 Abha, Saudi Arabia; Ioannis Valais, PhD, Department of Medical Instrument Technology, Technological Educational Institution of Athens, Ag Spyridonos and Dimitsanis, Egaleo, Athens, 12210, Greece
S- Editor Cheng JX L- Editor Webster JR E- Editor Zheng XM
| 1. | Xue F, Michels KB. Intrauterine factors and risk of breast cancer: a systematic review and meta-analysis of current evidence. Lancet Oncology. 2007;8:1088-1100. |
| 2. | Wolfe JN. Breast patterns as an index of risk for developing breast cancer. AJR Am J Roentgenol. 1976;126:1130-1137. |
| 3. | American College of Radiology ¨C Breast Imaging Reporting and Data System (BI-RADS). Atlas, 2006. |
| 4. | del Bimbo A. Visual information retrieval. San Francisco: Morgan Kaufmann Publishers Inc 1999; . |
| 5. | Doi K. Computer-aided diagnosis in medical imaging: historical review, current status and future potential. Comput Med Imaging Graph. 2007;31:198-211. |
| 6. | Rangayyan RM, Ayres FJ, Desautels JEL. A review of computer-aided diagnosis of breast cancer: Toward the detection of subtle signs. J Franklin Inst. 2007;344:312-348. |
| 7. | Tagare HD, Jaffe CC, Duncan J. Medical image databases: a content-based retrieval approach. J Am Med Inform Assoc. 1997;4:184-198. |
| 8. | Müller H, Michoux N, Bandon D, Geissbuhler A. A review of content-based image retrieval systems in medical applications-clinical benefits and future directions. Int J Med Inform. 2004;73:1-23. |
| 9. | Lehmann TM, Güld MO, Deselaers T, Keysers D, Schubert H, Spitzer K, Ney H, Wein BB. Automatic categorization of medical images for content-based retrieval and data mining. Comput Med Imaging Graph. 2005;29:143-155. |
| 10. | Baeza-Yates R, Ribeiro-Neto B. Modern information retrieval. Addison-Wesley Professinal, 1999. |
| 11. | Castella C, Kinkel K, Eckstein MP, Sottas PE, Verdun FR, Bochud FO. Semiautomatic mammographic parenchymal patterns classification using multiple statistical features. Acad Radiol. 2007;14:1486-1499. |
| 12. | Sheshadri HS, Kandaswamy A. Breast tissue classification using statistical feature extraction of mammograms. Med Imag Inform Sci. 2006;23:105-107. |
| 13. | Wang XH, Good WF, Chapman BE, Chang YH, Poller WR, Chang TS, Hardesty LA. Automated assessment of the composition of breast tissue revealed on tissue-thickness-corrected mammography. AJR Am J Roentgenol. 2003;180:257-262. |
| 14. | Bovis K, Singh S. Classification of mammographic breast density using a combined classifier paradigm. 2002; Medical Image Understanding and Analysis (MIUA) Conference, Portsmouth. |
| 15. | de Oliveira JEE, Güld M, de Albuquerque Araújo A, Ott B, Deserno T. Towards a standard reference database for computer-aided mammography. Proceedings of SPIE Medical Imaging, volume 6915. Proceedings of SPIE Medical Imaging, volume 6915. 2008: 69151Y. |
| 16. | Lehmann TM, Güld MO, Thies C, Fischer B, Spitzer K, Keysers D, Ney H, Kohnen M, Schubert H, Wein BB. Content-based image retrieval in medical applications. Methods Inf Med. 2004;43:354-361. |
| 17. | Heath M, Bowyer KW, Kopans D, Moore R, Kegelmeyer P. Current status of the digital database for screening mammography. Dordrecht: Kluwer Academic Publishers 1998; 457-460. |
| 18. | Suckling J. The mammographic image analysis society digital datagram database. Exerpta Medica International Congress Series. 1994;1069:375-378. |
| 19. | Center for Health Care Technologies Livermore. Lawrence Livermore National Library/UCSF Digital Mammogram Database. Livermore, CA, 1995. |
| 20. | Lehmann TM, Schubert H, Keysers D, Kohnen M, Wein BB. The IRMA code for unique classification of medical images. Proc SPIE. 2003;5033:440-451. |
| 21. | Castelli V, Bergman LD. Image databases: search and retrieval of digital imagery. New York: Wiley-Interscience 2001; . |
| 22. | Duda RO, Hart PE, Stork DG. Pattern classification. New York: John Wiley & Sons 2001; . |
| 23. | Gonzalez RC, Woods RE, Eddins SL. Digital image processing using MATLAB. New Jersey: Prentice-Hall 2003; . |
| 24. | Golub GH. Matrix computations. Johns Hopkins series in the matematicals sciences. 1983;. |
| 25. | Eldén L. Numerical linear algebra in data mining. Acta Numerica. 2006;15:327-384. |
| 26. | Wang Y, Tan T, Zhu Y. Face verification based on singular value decomposition and radial basis function neural network. Proceedings of Asian Conference on Computer Vision. Taipei, Taiwan; 2000. |
| 27. | Chen Q, Tai X, Dong Y, Pan S, Wang X, Yin C. Medical image retrieval based on semantic of neighborhood color moment histogram. In: The 2nd International Conference on Bioinformatics and Biomedical Engineering 2008; 2221-2224. |
| 28. | Akay MF. Support vector machines combined with feature selection for breast cancer diagnosis. Expert Syst Appl. 2009;36:3240-3247. |
| 29. | Vapnik VN. The nature of statistical learning theory. New York: Springer-Verlag 1995; . |
| 30. | Wong WT, Hsu SH. Application of SVM and ANN for image retrieval. Eur J Oper Res. 2006;173:938-950. |
| 31. | van Rijsbergen CJ. Information retrieval. London: Butterworth & Co 1979; . |
| 32. | Yang Y, Wei L, Nishikawa RM. Microcalcification classification assisted by content-based image retrieval for breast cancer diagnosis. In: IEEE International Conference on Image Processing 2007; 1-4. |
| 33. | Crammer K, Singer Y. On the learnability and design of output codes for multiclass problems. Computational Learning Theory. 2000;35-46. |
| 34. | Hsu CW, Lin CJ. A comparison of methods for multiclass support vector machines. IEEE Trans Neural Netw. 2002;13:415-425. |
| 35. | Suykens JAK, Gestel TV, Brabanter JD, Moor BD, Vandewalle J. Least squares support vector machines. Singapore: World Scientific 2002; . |
| 36. | Güld MO, Thies C, Fischer B, Lehmann TM. A generic concept for the implementation of medical image retrieval systems. Int J Med Inform. 2007;76:252-259. |
| 37. | Deserno TM, Güld MO, Plodowski B, Spitzer K, Wein BB, Schubert H, Ney H, Seidl T. Extended query refinement for medical image retrieval. J Digit Imaging. 2008;21:280-289. |
| 38. | Andrews H, Patterson C. Singular value decompositions and digital image processing. IEEE Trans Acoust Speech Signal Process. 1976;24:26-53. |
| 39. | Kinoshita SK, de Azevedo-Marques PM, Pereira RR Jr, Rodrigues JA, Rangayyan RM. Content-based retrieval of mammograms using visual features related to breast density patterns. J Digit Imaging. 2007;20:172-190. |
| 40. | Davis J, Goadrich M. The relationship between precision-recall and roc curves. New York, NY: ACM 2006; 233-240. |