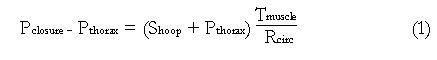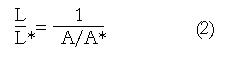Published online Mar 7, 2007. doi: 10.3748/wjg.v13.i9.1335
Revised: February 3, 2007
Accepted: February 8, 2007
Published online: March 7, 2007
We summarize from previous works the functions of circular vs. longitudinal muscle in esophageal peristaltic bolus transport using a mix of experimental data, the conservation laws of mechanics and mathematical modeling. Whereas circular muscle tone generates radial closure pressure to create a local peristaltic closure wave, longitudinal muscle tone has two functions, one physiological with mechanical implications, and one purely mechanical. Each of these functions independently reduces the tension of individual circular muscle fibers to maintain closure as a consequence of shortening of longitudinal muscle locally coordinated with increasing circular muscle tone. The physiological function is deduced by combining basic laws of mechanics with concurrent measurements of intraluminal pressure from manometry, and changes in cross sectional muscle area from endoluminal ultrasound from which local longitudinal shortening (LLS) can be accurately obtained. The purely mechanical function of LLS was discovered from mathematical modeling of peristaltic esophageal transport with the axial wall motion generated by LLS. Physiologically, LLS concentrates circular muscle fibers where closure pressure is highest. However, the mechanical function of LLS is to reduce the level of pressure required to maintain closure. The combined physiological and mechanical consequences of LLS are to reduce circular muscle fiber tension and power by as much as 1/10 what would be required for peristalsis without the longitudinal muscle layer, a tremendous benefit that may explain the existence of longitudinal muscle fiber in the gut. We also review what is understood of the role of longitudinal muscle in esophageal emptying, reflux and pathology.
-
Citation: Brasseur JG, Nicosia MA, Pal A, Miller LS. Function of longitudinal
vs circular muscle fibers in esophageal peristalsis, deduced with mathematical modeling. World J Gastroenterol 2007; 13(9): 1335-1346 - URL: https://www.wjgnet.com/1007-9327/full/v13/i9/1335.htm
- DOI: https://dx.doi.org/10.3748/wjg.v13.i9.1335
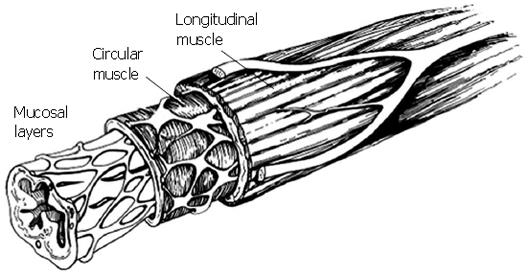
Figure 1 is a schematic of the cross section of the esophagus. The muscularis propria is comprised of a layer of circularly aligned muscle fibers within, and a layer of longitudinally aligned muscle fibers without, surrounding mucosal layers of loosely connected tissue. The muscle mass of the circular and longitudinal muscle layers is nearly the same. In the resting state, the circumferentially averaged thickness of the muscularis has been measured by various researchers as 1.1-1.4 mm in the esophageal body, and 1.9-2.4 mm in the abdominal esophagus near the junction with the gastric cardia[1-6].
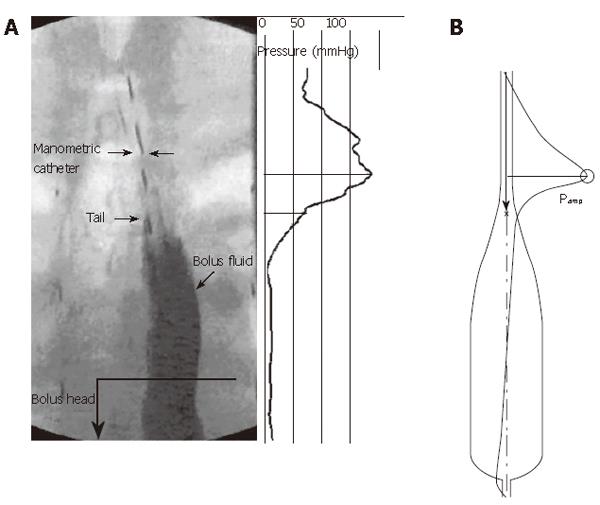
The function of the circular muscle layer of the esophageal muscularis propria is clear. Esophageal peristalsis (as well as segmental contraction in the intestines) requires luminal closure against the resisting forces within a viscous bolus, demanding the existence of circumferential, or “hoop” stresses to generate applied pressures at a level sufficient to squeeze the lumen closed[7]. “Peristalsis” implies that the circular muscle contraction travels as a wave along the esophageal lumen to create a traveling contraction wave and a moving point of luminal closure that forces the bolus fluid ahead, and ultimately into the stomach[7,8]. As indicated in Figure 2, peristalsis generates fluid pressure at the mucosal surface equal to the closure pressure from circular muscle hoop stress. A similar plot can be created for luminal frictional shear stress[8]. Within the bolus fluid pressure must generally decrease in the direction of fluid motion to force the fluid forward against frictional resisting forces in this friction-dominated flow. The axial pressure gradient is very small in the distended part of the bolus, but becomes very sensitive to luminal radius as the fluid layer thins[7]. Near the moving point of closure, fluid pressure rises in response both to the radial closure force and to frictional stresses associated with the forcing of fluid from the point of closure[7,8]. Proximal to the bolus tail (Figure 2), the circular muscle squeezes against the mucosae, which are forced onto a thin layer of residual liquid that lubricates the interface between the mucosa and manometric catheter surface (and, in the absence of a catheter, fills pockets within the mucosal folds). Above the tail, pressure rises in direct response to the tonic component of hoop stress within the circular muscle layer[9].
However, the mass of the esophageal muscularis propria is split evenly between circular and longitudinal muscle fiber[1,2]. What, then, is the role of longitudinal muscle in the esophagus, and why is it there? This is the question that we, at least partially, address in this integrative summary of current understanding.
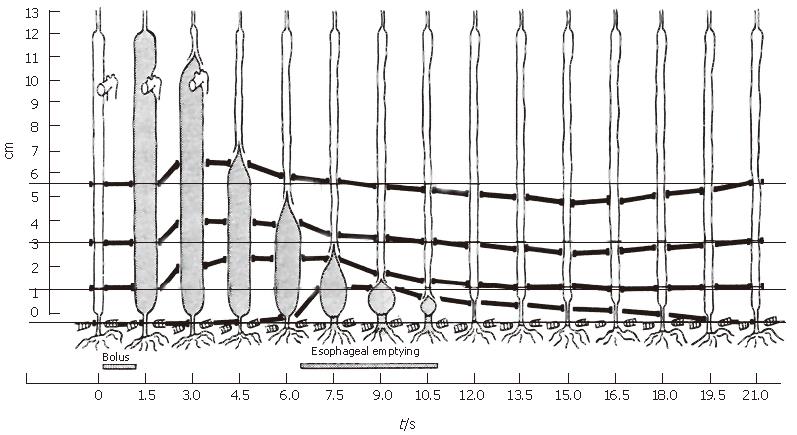
Consider in Figure 3 the classic data of Dodds et al[10] in which four metal markers were sewn into the wall of the lower esophagus of cats and tracked radiographically during swallows. They found that shortly after the initiation of the swallow, all markers except for the one at the hiatus shifted orally together, implying longitudinal shortening of the upper esophagus. Because only longitudinally aligned muscle fibers can generate the active tension necessary to shorten the upper esophagus, we conclude that longitudinal muscle in the upper esophagus has contracted locally during the initial period after a swallow. As the bolus tail passed a wall marker in the lower esophagus, the marker moved aborally, and the relative distance between pairs of markers surrounding the tail shortened, implying local shortening of longitudinal muscle fibers. The process continued as the bolus tail progressed distally, until it approached the hiatus, at which time the hiatal marker was pulled orally, an ampulla formed[11], and esophageal emptying began. Still the relative distance between adjacent markers surrounding the bolus tail decreased as the intrinsic lower sphincter was pulled into the thoracic cavity and then returned to its original position well after emptying was complete.
Basic features of the marker motions observed in the feline esophagus by Dodds et al[10] have also been observed more crudely in various studies in the human esophagus where 11 mm metal clips were attached to the mucosal surface and observed fluoroscopically during liquid swallows[12-15]. Pouderoux et al[14], in particular, using three clips in the distal esophagus, observed initial stretch followed by shortening during bolus transport, consistent with Figure 3.
We address here the questions: (1) how does longitudinal muscle contract locally in the human esophagus during peristalsis, (2) is the contraction coordinated in any way with peristaltic contraction of the circular muscle, (3) why does longitudinal muscle contract during esophageal peristalsis, and (4) are there benefits to longitudinal muscle contraction that are of sufficient importance to explain the existence of a longitudinal muscle layer comprising nearly half the total muscle mass? To answer these questions we integrate the literature with two studies which apply basic laws of mechanics, endoluminal ultrasound, and a mathematical model, to analyze local contraction of longitudinal muscle in the esophagus during peristaltic transport. We follow with a review of other studies relevant to esophageal longitudinal muscle function and close with a summary discussion and speculation on at least one reason why evolution has created a gut with a longitudinal muscle layer as massive as the circular muscle layer that clearly underlies gut function.
Circumferential “hoop” stress in the esophageal wall is a summation of neurologically induced active stress (or “tone”) in the circular muscle, a passive elastic contribution resulting purely from muscle distension, and a contribution that arises from external pressures on the muscle surfaces. Changes in hoop stress are directly reflected in changes in intraluminal “closure” pressure, so that manometric measurement of intraluminal pressure can be used in the study of the mechanics and physiology of circular muscle tone. This is especially the case near the bolus tail where passive contributions are negligible and pressure reflects directly the active stress component[9].
The relationship between intraluminal pressure and hoop stress is given by a Newton’s law force balance across the esophageal wall, as illustrated in Figure 4. The following is an exact expression for a cylindrical esophagus with hoop stress entirely within the muscularis propria (Figure 4)
Math 1
Pclosure is the pressure at the mucosal-fluid interface required to maintain closure and Shoop is the total average hoop stress (force per unit muscle area) across the muscle layers (muscularis propria), Tmuscle is the total thickness of the muscle layers, Rcirc is the radius to the inner surface of circular muscle, and Pthorax is the pressure in the thoracic cavity external to the esophageal lumen. Equation (1) is a good approximation for the real noncylindrical esophagus when the stress and thickness are interpreted as averages over both the thickness and circumference of the muscle layer, and therefore only dependent on the axial distance x along the lumen (Figure 2). (Note that the “Laplace law” is derived from equation (1) by assuming that Tmuscle is very much smaller than Rcirc. This is never the case, however, in a contracted gut segment[16]).
Equation (1) shows that relative intraluminal pressure (Pclosure - Pthorax) increases in direct proportion to hoop stress (Shoop) in the fully contracted regions, so that the inner circular muscle radius Rcirc is fixed, to the extent that the muscle thickness (Tmuscle) does not change with change in hoop stress. Experimentally, therefore, we interpret manometrically measured changes in pressure as indicating changes in circular muscle tone. As will be discussed next, these measurements have been made together with quantifications in local shortening of longitudinal muscle fibers, with implications on the assumption of fixed muscle thickness during contracted esophageal segments.
Whereas intraluminal pressure responds to circular muscle tone because of the force balance involving hoop stress and intraluminal pressure, there is no corresponding balance between longitudinal stress and intraluminal pressure in a tubular esophagus. Manometry therefore provides no direct information on longitudinal muscle. The only way to measure longitudinal muscle stress directly is the implantation of strain gauges within the muscle wall. This has been done in an animal model[17], but cannot be done in humans. In humans the only approach currently available to measure longitudinal muscle contraction is indirect, through the measurement of relative changes in longitudinal wall displacement, as shown in Figure 3. Because muscle can only contract in response to neurological stimulation of muscle tone, the shortening of a localized axial segment implies one of two possible scenarios. In a previously unstimulated esophagus, local longitudinal shortening implies a local increase in active stress (tone) in the longitudinal muscle fibers within the shortened segment. In a longitudinally stimulated esophagus, local shortening of one axial segment produces stretching in adjacent segments; shortening of previously stretched segments, therefore, can arise from relaxation of a previously contracted adjacent segment. Local longitudinal shortening can therefore be used indirectly to indicate longitudinal muscle contraction when the history of longitudinal shortening is understood. To estimate longitudinal muscle stresses, would require a more complex integration of measurement with the laws of mechanics and modeling[9] than is possible from the simple force balance that produced equation (1).
In a number of studies, to measure longitudinal shortening of esophageal segments in humans, metal clips have been applied to the epithelial surface and their axial motions measured radiographically[12-15]. Whereas all of these studies are at lower spatial resolution and contain less detail than the Dodds et al[10] study in the cat (Figure 3), the results are consistent. Technical difficulties and lack of comfort during the endoscopic placement of clips has limited the application to 1-3 clips. Furthermore, the clips are large (11 mm), and the relative change in length between two clips typically spaced 3-5 cm is an average over the clip spacing, and has been shown to be a significant underestimate of more localized longitudinal shortening[1]. Finally, since clips mark the motion of the mucosal surface, which moves relative to the muscularis, there is inherent uncertainty in the interpretation of relative clip motion as inferring muscle shortening.
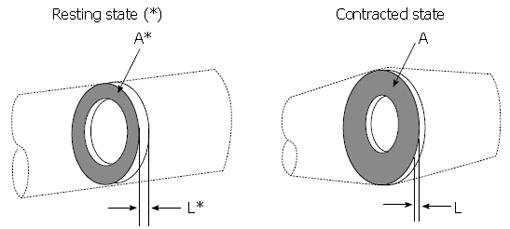
The practical limitations of clips can be avoided by combining a basic law of mechanics with the measurement of muscle cross section with endoluminal ultrasound (EUS) imaging of the esophageal muscle cross section. The principle is illustrated in Figure 5. Imagine a thin slice of the muscularis propria at some axial location, x, in the resting state (denoted by*), and the same slice containing the same muscle mass at some later time, for example during the passage of a contraction wave (no*). Muscle is a mixture of liquid and solid material within the mixture muscle fiber, collagen, etc., which are incompressible, meaning that the density (mass per unit volume) is always the same. Thus, since the mass of the slice in Figure 5 is the same before and after contraction, so is the volume (volume = mass/density). The volume of the slice is the cross sectional area times its thickness, so that L*A* = LA. The relative shortening of the slice is L/L*, which is therefore given by:
Math 1
A decrease in the longitudinal shortening parameter L/L*, or equivalently an increase in A/A*, quantify longitudinal muscle shortening localized to the axial position of the measurement.
To quantify local longitudinal shortening (LLS), one measures the cross-sectional areas of the muscle layer in the relaxed state (A*) and during contraction (A) using endoluminal ultrasound (EUS) and image analysis methods. Nicosia et al[1], using the data of Miller et al[4], and Dai et al[2] used a custom assembly that combined high-frequency ultrasound with water-perfused manometry to collect esophageal segment cross-sectional images simultaneously with intraluminal pressure. A 20 MHz ultrasonographic transducer, placed within a 6 French catheter, rotated at 15-30 Hz to provide 360 degrees esophageal cross-sectional imaging with a 0.1 mm axial slice thickness and a typical penetration depth of 2 cm was used. Images were recorded on super VHS videotape at 30 frames/s. To quantify intraluminal pressure at the same location, a second, 3 French angiography catheter was glued to the EUS catheter and a small side-hole was made at the same level as the ultrasound transducer for perfused manometry. The two data sets were synchronized to within one video frame when recorded on a Kay Elemetrics swallowing workstation. The video images were digitized at 30 frames/s in single byte uncompressed tiff format and pressure was digitized at 250 Hz.
It should be noted that with EUS one measures local longitudinal shortening at a fixed axial location, similar to pressure measurement with manometry. Figure 3 shows that the muscle material moves axially relative to the point of measurement associated with longitudinal shortening in the axial segment surrounding the point of measurement.
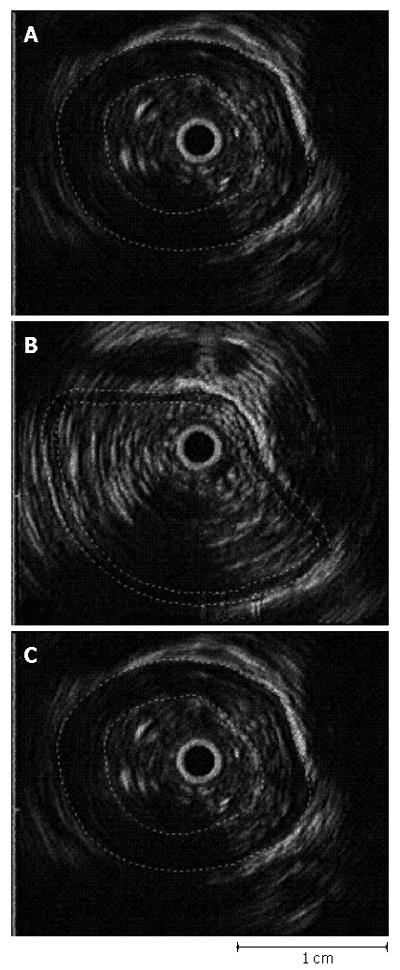
Figure 6 is an example of cross sections of the esophagus as seen from EUS (A) in the resting state, (B) while the head of the bolus passes the EUS transducer, and (C) when the peak intraluminal pressure passes the transducer [ref. 1]. The black circle with white outline in the center of each image is the EUS transducer. In each image, the inner boundary of the circular muscle and the outer boundary of the longitudinal muscle were outlined and the coordinates obtained using specially designed edge-detection software with a graphic user interface for interactive semi-automated edge detection[1]. In addition to extracting the muscle boundaries, the white band that identifies the interconnective tissue at the interface between the two muscle layers was quantified. (Because the boundary between the circular and longitudinal muscle layers was generally less visible than the inner and outer boundaries of the muscularis, the accuracy of the digitized coordinates of the interconnective tissue layer was correspondingly less accurate).
In each image a pie-shaped black area facing outward from the catheter towards the bottom of each image is produced as a result of the manometric catheter interfering with the acoustic wave. To objectively define the muscle edges through this black area, the missing data were estimated using cubic spline interpolation from the portions of the detected edges on each side of the missing segment (Figure 6). The edges were always superimposed on the image and the user adjusted segments incorrectly extracted by the automated image-analysis system. Consequently, the human time required to segment the hundreds of images needed was very high, limiting the number of images that could be quantified. In the end, Nicosia et al[1] segmented and quantified several hundred images over the entire swallowing sequence with four normal subjects.
From the digitized coordinate data of the three edges from each image the cross sectional areas of the total muscle area, as well as the individual circular and longitudinal muscle areas, were quantified. Given the difficulties in the accurate estimation of the interconnective tissue on many of the images, the accuracy of the quantification for the individual longitudinal and circular muscle areas was less than the accuracy of the entire muscle area. However, quantification of total muscle area, and therefore the LLS shortening parameters A/A* and L/L* with equation (2), are felt to be quite accurate. Furthermore, only this approach allows for direct quantification of the local longitudinal shortening of esophageal muscle layers.
In Figure 2A we show interpolated high-resolution manometry data plotted axially along the lumen during peristaltic transport. Not surprisingly, the pressure is highest in the zone of complete occlusion, just proximal to the bolus tail. The measured pressure is, in reality, within a thin liquid film between the manometric catheter and mucosa. Equation (1) gives the relationship between the fluid pressure, muscle stress, and geometry. Thus, the stress required by the muscles to close the lumen above the bolus tail is the pressure within the bolus fluid in the closed lumen. This fluid pressure is determined by the details of bolus fluid motion in response to the motion of the mucosal surface that, in turn, moves the bolus fluid and generates pressure and resisting frictional forces at the fluid-epithelial interface. The motion of the mucosal surface originates in circular muscle contraction moving the mucosal surface radially (transverse to the lumen), and in longitudinal muscle contraction moving the surface axially (along the lumen).
We ask the following functionally important questions: If longitudinal muscle contracts locally, coordinated in some way with circular muscle contraction during peristalsis, does the resulting motion of the mucosal surface in any way alter the pressure force that maintains luminal closure (Pclosure in equation 1)? If so, is the alteration beneficial or detrimental to the efficacy of peristalsis? These questions cannot be answered experimentally, because it would be necessary to repeat the experiment with circular muscle contraction precisely the same in all experiments, but with the degree of longitudinal muscle contraction suppressed without altering circular muscle physiology. However, a physics-based mathematical model of peristaltic fluid transport can be applied to fill in certain gaps between experimentally measurable data to address questions inaccessible to experiment. (By “physics-based, we mean modeling derived directly from the laws of physics which, in mathematical form, are predictive.) To answer the questions above we therefore integrate a mathematical model of bolus fluid motion with image and pressure data of esophageal bolus transport. In this section we describe this model in general terms without mathematical equations. Mathematical details can be found in Pal & Brasseur[18] and Li & Brasseur[8].
Figure 2B shows a prediction of intraluminal pressure for bolus transport with a bolus shape designed as representative of esophageal peristalsis. The modeled bolus geometry is an idealized version of the physiological bolus shape (Figure 2A) in order to capture the essential elements of esophageal bolus transport needed for the study. These essential elements are: (1) Accurate mathematical representation of Newton’s second law of mechanics applied to liquid bolus motion, intrabolus pressure, and intrabolus frictional stress, driven by the motion of a lumen boundary surrounding the bolus liquid. A basic discussion of these physical effects in esophageal bolus transport is give in[7]; (2) Specification of a “tear-drop” bolus shape at specified peristaltic wave speed that is representative of the actual bolus during peristalsis. As discussed by Li & Brasseur[8], near the bolus tail there is a coupling between the bolus shape and the pressure that, through equation (1), reflects the manner in which circular muscle stress increases to a peak proximal to the bolus tail[9]. The basic nature of peristaltic muscle squeeze produces a “tear-drop” shaped bolus, as shown in fluoroscopic imaging of bolus transport (e.g., Figure 2A) and as modeled in Figure 2B; (3) The diameter of the modeled esophageal lumen in the fully contracted region proximal to the bolus tail is a direct reflection of the liquid layer that coats the manometric catheter as in Figure 2A, or lubricates the mucosal folds during transport. In the model, this occlusion diameter is an “effective” lubrication layer that, for given peristaltic wave speed, reflects the maximum squeeze of the circular muscle[7]. Peak muscle squeeze pressure is adjusted to match experiment by adjusting this occlusion diameter; (4) For the purposes of this study, the most important advantage of the mathematical model is the ability to fully specify the longitudinal motions of the lumen surface. We do this consistent with measured local shortening of longitudinal muscle and measured coordination with circular muscle contraction. However, we explore the consequences of local longitudinal shortening (LLS) with our unique ability, with the model, to systematically alter the contribution of LLS to contractile pressure, from no contribution to the measured physiological contribution, as well as to systematically explore the consequences of alignment and misalignment between longitudinal and circular muscle contraction. Through this unique property of a mathematical model, we are able to explain mechanical function of longitudinal muscle that is difficult to explain through experiment alone.
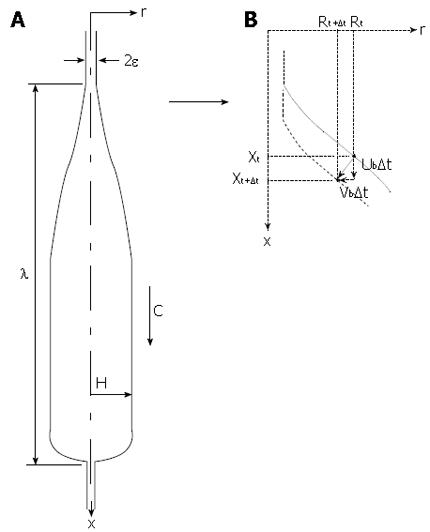
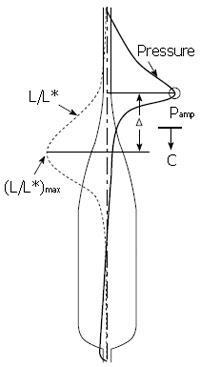
Figure 7 shows the basic elements and parameters of the mathematical model. The esophageal geometry is simplified to a straight axisymmetric deformable tube along which a bolus of fixed shape travels at wave speed c. Deviations from axisymmetry are unimportant to the effects of longitudinal muscle function that interest us here. The volume of the bolus, bolus length λ and radius H are specified consistent with fluoroscopic imaging of esophageal bolus transport. As discussed above, lubrication thickness, Ε, is specified consistent with manometric measurement of peak closure pressure, Pamp (Figure 2).
To study the effects of local longitudinal shortening on closure pressure, the space-time motions of the surface of the mucosa are explicitly specified in the model calculation to be consistent with (1) no longitudinal shortening, (2) the EUS and clip measurements of LLS, and (3) systematic variations in level of LLS between no shortening and the measured levels of shortening. In addition we systematically vary the degree of coordination between local circular muscle contraction, and LLS. As illustrated in Figure 7B, in the model we ultimately specify the axial (Ub) and radial (Vb) velocities of each surface point along the axial coordinate (x) and time (t). The standard model of esophageal bolus transport does not include longitudinal shortening, so there is no axial motion in the model (Ub = 0).
With longitudinal shortening, the axial velocity is made nonzero consistent both with the shape of the propagating bolus, and with measured LLS consistent with the EUS results of Nicosia et al[1], and the marker studies of Dodds et al[10], Pouderoux et al[14]. and Shi et al[15]. These will be discussed in the following section.
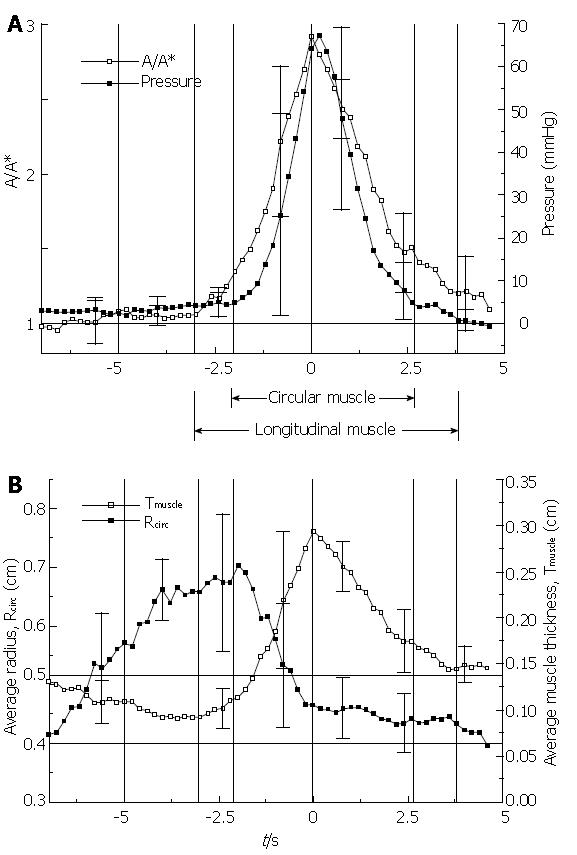
Figure 8 shows the essential result from the EUS analysis of Nicosia et al[1]. By making use of conservation of muscle mass, equation (2), the LLS parameter A/A* is plotted against time together with intraluminal pressure during the transport of 10 mL liquid boluses through the mid esophagus (Figure 8A). An increase in A/A* implies a decrease L/L*, a local shortening of the esophageal segment at the axial location of the ultrasound transducer. From equation (1) and the analysis in[9], we may interpret the variation in intraluminal closure pressure as a close approximation to the variation in circular muscle hoop stress, or tone. In Figure 8B are plotted the average muscle thickness, Tmuscle, and the luminal radius to the circular muscle, Rcirc, in the same time axis as Figure 8A. Ensemble averages were carried out over four normal subjects with the time reference as the peak in A/A*, or maximum LLS.
The Nicosia et al[1] result (Figure 8) is important for several reasons. It tells us that during peristaltic transport of a bolus through the mid esophagus, longitudinal muscle contracts and shortens in a highly localized manner that is tightly coordinated with the contraction of the circular muscle. At a fixed axial location within the esophagus, longitudinal muscle contraction precedes circular muscle contraction, but longitudinal muscle maximally shortens coincident with maximum circular muscle contraction. Longitudinal muscle then relaxes, but more slowly than circular muscle. The Nicosia et al[1] result in the mid esophagus has recently been replicated by Mittal et al[19] at 5 and 10 cm above the LES. We can relate this result to the marker studies in the cat by Dodds et al[10] in Figure 3 where the time of maximal shortening of the three marked segments always occurred when the bolus tail was between the markers. Combined with the more precise result of Figure 8, we conclude that esophageal peristalsis may be described as overlapping peristaltic waves of circular and longitudinal muscle contraction that are spatially aligned so that peaks in longitudinal and circular muscle contraction occur nearly together as the two waves propagate concurrently along the esophageal lumen. The in vivo-modeling study by Nicosia & Brasseur[9] showed that the spatial pressure distribution surrounding the bolus tail in Figure 2 is a good approximation of hoop stress. If it were possible to plot local stress in longitudinal muscle on the same plot, Figure 8 suggests that the local longitudinal stress distribution would peak at the same place as hoop stress and pressure in Figure 2, but would be broader-LLS would envelope circular muscle contraction as the peristaltic waves propagate along the esophageal body.
Figure 8B indicates that as the bolus distends the esophagus, a thinning of the muscularis occurs with no change in the muscle cross sectional area, and therefore without LLS. The initiation of LLS coincides with transition from a thinning to a thickening muscle layer, while the initiation of circular muscle contraction coincides with the transition from a distending to a closing lumen. When the lumen is fully closed, change in muscle thickness implies change in muscle area, however the true marker of LLS is relative change in cross sectional muscle area rather than thickness.
Note in Figure 3 that the distal segment of the cat esophagus initially lengthens, then shortens longitudinally as the bolus tail (just distal to the point of peak circular/longitudinal muscle contraction) approaches. This initial lengthening has also been measured with clips in the distal human esophagus[14,15], but is not observed in the data of Figure 8 from the mid esophagus (nor in[19]). The initial lengthening appears to result from a pulling on the distal esophagus from above against an initially immobile LES, until the bolus tail enters the mid esophagus (Figure 3) and forms an ampulla, preceding the opening of the hiatus and esophageal emptying[11]. Ghosh et al[20] used a combination of concurrent manometry/fluoroscopy data and mathematical modeling of the process of hiatal opening and esophageal emptying to show that the circular muscle of the distal esophagus undergoes a rapid increase in tone that rapidly raises intrabolus pressure to force open the relaxed sphincter segment, and then maintains high pressure while bolus fluid is driven through the hiatus and into the stomach.
Ghosh et al[20] argued that longitudinal shortening plays a role in this process by pulling the intrinsic component of the smooth muscle sphincter orad and over the surface of a forming ampulla, as suggested by the Dodds et al[10] data in Figure 3. Since sphincteric smooth muscle is designed to maintain tone in the resting contracted state, it is well suited to the generation of sustained tone over an ampulla, as needed during esophageal emptying. The hypothesis, therefore, is that the active suppression of LES tone ceases not when the LES returns to its resting state after esophageal emptying, but rather before emptying begins as the LES is pulled orad and placed over the ampulla surface by contraction of longitudinal muscle in the esophageal body. In this way, the LES contributes to the opening of the hiatus by increasing intrabolus pressure during ampulla formation, and to transsphincteric flow by the maintenance of high ampullary pressure. It would follow, then, that immobilizing the LES with fundoplication may explain the insufficient generation of muscle tone required to open the hiatus and drive esophageal emptying and, consequently, to fully empty the esophagus with a single peristaltic wave as has been consistently observed.
A question of mechanics now arises: how is it that the LES is not pulled orad until the peristaltic circular/longitudinal muscle waves enter the distal esophagus? Why does the LES initially remain at its resting position? Newton’s second law states that the LES will move orad only if there is an orad force on the sphincteric segment of esophagus that overbalances a caudal force. Apparently, until the bolus tail passes into the distal-most esophagus, the upward pull of the esophageal body on the sphincteric segment is insufficient to overcome the caudal pull of the phreno-esophageal ligaments. However, as the peristaltic wave enters the lower esophagus, the balance of forces on the sphincteric segment must change. Given that the phreno-esophageal ligaments are purely elastic elements, and therefore cannot generate tone, it must be the case that the total upward force supplied by the longitudinal muscle must increase as the peristaltic circular/longitudinal wave approaches the hiatus and an ampulla forms. This conclusion is supported by Dai et al[2] who measured A/A* at peak intraluminal pressure at different distances from the LES during swallowing of 5 mL boluses. Their result is shown in Figure 9; the level of local longitudinal shortening increases as the peristaltic wave passes into the lower esophagus, suggesting a corresponding increase in orad longitudinal stress on the gastro-esophageal segment. Longitudinal muscle, therefore, appears to play an important functional role in the process of hiatal opening and esophageal emptying.
However, there is another, more important, role for concurrent local longitudinal shortening and circular muscle peristaltic contraction waves, that we describe next.
As discussed above in context with equation (1), the pressure required to maintain closure proximal to the bolus tail is generated by an integration of circular muscle hoop stress over the muscle thickness, which represents a summation of the forces of the individual circular muscle fibers on the cross section illustrated in Figure 4. It follows that if a longitudinal segment of the esophagus shortens, circular muscle fibers will be compressed within a narrower longitudinal segment and the number of fibers that contribute to hoop stress in that narrowed segment increases. Consequently, the total force available to maintain closure is larger for the same individual fiber force by the increase in number of fibers within the narrow segment. Conversely, for a given total closure force required to maintain the closure of a fixed longitudinal segment, local longitudinal shortening will reduce the force per circular muscle fiber by the increase in the number of circular muscle fibers recruited to create that given closure force.
Figure 8A shows a maximum local longitudinal shortening of L/L* = 1/(A/A*) ≈ 1/3. This implies three times more circular muscle fibers available for generating closure pressure after LLS, which reduces the force required by each fiber by 1/3. This is a substantial savings in force, and correspondingly energy required to effect esophageal peristalsis. This increase in longitudinal density of muscle fibers might be described as a “physiological” explanation for the existence of a longitudinal muscle layer[1].
Another way to make the same argument is through the force balance, equation (1), and Figure 4. Above the bolus tail, the radius Rcirc remains fixed. Up to now we have focused on the relationship between hoop stress (Shoop) and closure pressure (Pclosure) in equation 1. However, local longitudinal shortening increases the cross sectional muscle area A ≈ (2πRcirc)Tmuscle, so that increasing the area by a factor of three (Figure 8A) with fixed Rcirc also increases the thickness by roughly a factor of three. Thus, for the same closure pressure, Pclosure, the hoop stress, and therefore average fiber force, can reduce by at least a factor of three.
However, equation (1) also produces the following question: Is the closure pressure Pclosure the same with local longitudinal shortening as without? That is, if evolution had not created a longitudinal muscle layer, would the pressure required to maintain closure (left side of equation 1) be the same? The reason why the closure pressure might be different is that a traveling wave of LLS causes the mucosal surface to move axially (Figure 3). As the bolus tail approaches a material point on the mucosal surface, the material point moves orad; then, as the tail passes that material point, it reverses direction and moves caudal. Because there is a thin liquid film above the tail the pressure in the tail region is very sensitive to tail geometry[8], so that axial motions of the mucosal surface close to the tail have the potential to impact fluid pressure and frictional stresses there. It might be the case, for example, that the pressure near the tail required to maintain closure is higher as a result of the axial motions associated with LLS than without in which case, the gain in muscle fiber force from the compression of muscle fibers by physiological stimulation of longitudinal muscle would be offset by an increase in closure pressure. So, the answer to the question is important for the role of longitudinal muscle in esophageal peristalsis. However, these questions cannot be answered through in vivo experiment, so we employ the power of mathematical modeling to extend data measurable in vivo to data unavailable to physiological experiment.
The basic mathematical model[18] from which closure pressure can be predicted was described in “MATERIALS AND METHODS” above and the basic parameters of bolus motion are shown in Figure 7. However, the axial motions of the lumen surface in the model were described only in general terms, in the absence of the local longitudinal shortening data from Figure 8. These data were used to specify and parameterize the boundary axial and radial velocities Ub and Vb of all material points on the modeled mucosal surface. LLS was modeled as a longitudinal muscle contraction wave that propagates together with the circular muscle contraction wave, as illustrated in Figure 10. The longitudinal muscle contraction wave was modeled as a longitudinal shortening wave with specified shape L/L*vs axial coordinate x that moves with the specified luminal geometry at the same bolus speed c. The peak in LLS was displaced from peak intraluminal pressure by the specified amount ∆. The shape and width of L/L* were determined from the data of Figure 8A, assuming a wave speed of 3 cm/s (typical for bolus transport through the mid esophagus). Peak LLS, (L/L*)max, was varied: from no shortening (L/L* = 1, implying no axial motion of the mucosal surface, or Ub = 0), to the physiological value of shortening, (L/L*)max = 0.35), leading to surface motions similar to the upper markers in Figure 3. The displacement between the longitudinal and circular muscle contraction waves, ∆ (Figure 10), was also systematically varied from 0 to ± 2 cm. The mathematical details are given in[18].
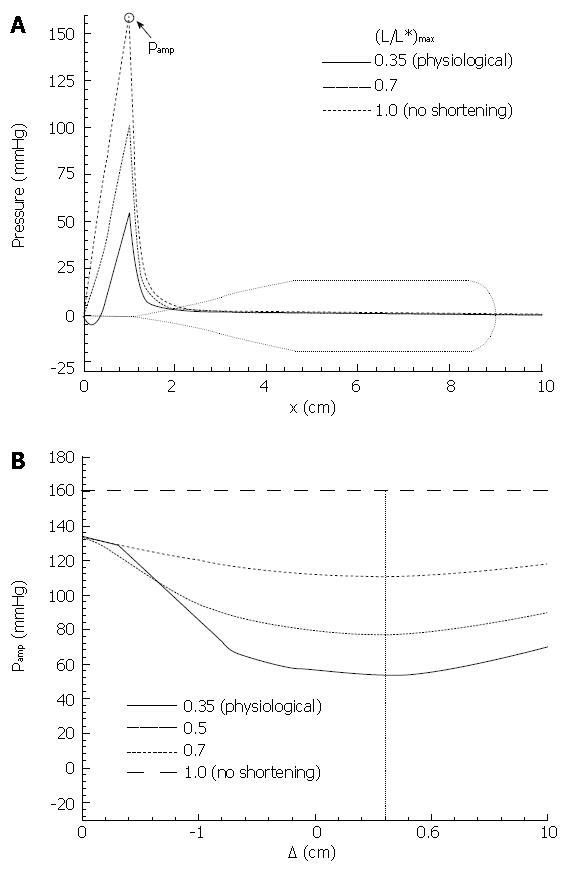
The primary result from Pal & Brasseur[18] is given in Figure 11. In Figure 11A closure pressure is plotted along the bolus axis for different levels of local longitudinal shortening, with the longitudinal and circular muscle contraction waves perfectly aligned (∆ = 0). The lubrication layer thickness Ε was fixed at a value where peak closure pressure in the absence of LLS was roughly 150 mmHg. We discover that a coordinated peristaltic wave of local longitudinal shortening reduces peak closure pressure progressively, and very significantly, with increasing levels of LLS. At the physiological level of LLS measured by Nicosia et al[1], the level of pressure required to maintain closure is one third what would be required in the absence of a longitudinal muscle wave coordinated with the circular muscle peristaltic wave. This is a very substantial reduction in the pressure required to maintain the same level of luminal closure, and is a fully mechanical effect that arises from the changes in fluid stresses that arise from relatively subtle axial movements of the lumen surface induced by the LLS associated with longitudinal muscle peristalsis.
In Figure 11B we plot the effect of displacement between the peak LLS and circular muscle contraction waves on peak closure pressure, for different levels of LLS. Whereas the minimum is relatively broad, we find that the effect of LLS on reduction of closure pressure is maximal when the circular and longitudinal muscle contraction waves are aligned to within roughly 1 cm, or on a time axis within about 1/3 second, consistent with Figure 8A.
Using a combination of intraluminal ultrasound with image analysis, the laws of mechanics, and mathematical modeling, we have arrived at a convincing functional explanation for the existence of longitudinal muscle in the esophagus. Combined longitudinal-with-circular-muscle peristaltic contraction waves have two beneficial multiplicative consequences to the circular muscle tone and energy required for esophageal peristalsis. Firstly, local contraction of longitudinal muscle shortens the longitudinal dimension of axial segments and increases the concentration of circular muscle fibers at the location of maximal circular muscle squeeze by nearly a factor of 3, thus reducing the force required by each circular muscle fiber by nearly 1/3 as compared to the same esophagus without the longitudinal muscle layer. Secondly, the local axial motions of the mucosal surface induced by a peristaltic wave of local longitudinal shortening reduce the level of applied pressure required to locally close the lumen also by roughly a factor of three, a result of the local changes in fluid stresses within the lubrication layer. The net result is an overall reduction of fiber force by about 1/9, or roughly 10% what would have been required in the absence of the longitudinal muscle layer! To obtain this benefit, longitudinal muscle contraction envelopes circular muscle contraction.
Furthermore, given that the power required by individual muscle fibers to transport a bolus through the esophagus is proportional to the fiber force, the coordination of longitudinal and circular muscle peristaltic waves greatly reduces the energy requirements for circular muscle fibers. Because the reduction in fiber force is so high, even when the additional power requirements of longitudinal muscle are taken into account, the net savings in energy requirements are substantial. Indeed the combined physiological and mechanical benefits are so great that one might extrapolate this observation as a potential explanation for the existence of longitudinal muscle and local longitudinal muscle shortening throughout the GI tract, including the intestines and sphincters.
Having understood how to interpret EUS data in context with LLS, EUS research preceding the Nicosia et al[1] study can now be interpreted in context with the discussions above. Furthermore, three additional studies involving clips provide additional insight.
Miller et al[4] were the first to report measurements of muscle thickness concurrent with intraluminal pressure during esophageal bolus transport. They report results essentially equivalent to the thickness and pressure results in Figure 8, showing an increase and decrease in muscle thickness surrounding the pressure as in Figure 8. In a more recent study, Dai et al[21] showed that the time period of circular muscle contraction with bolus transport through the esophageal body, as inferred from the duration of the peristaltic pressure, is strongly correlated to the time period of longitudinal muscle contraction as inferred from LLS (r = 0.92), further confirming the integration of longitudinal and smooth muscle contraction in esophageal peristalsis.
In an interesting study of concurrent changes in pressure and muscle thickness above and below local balloon distension of the esophagus above the LES, Yamamoto et al[22] showed that a peripherally induced increase in circular muscle tone above local balloon distension is strongly correlated with a local increase in muscle thickness. Below the balloon distension neither pressure nor muscle thickness increased. Because these studies were carried out in the absence of a bolus, we may interpret the increase in thickness as an increase in muscle cross sectional area, and therefore the presence of local longitudinal shortening above the distension, but not below. We conclude that a strong correlation exists between circular and longitudinal muscle contraction associated with local discussion. Based on studies of primary peristalsis, it is reasonable to hypothesize that the correlation between circular and longitudinal muscle contraction is maintained after balloon deflation and the initiation of secondary peristalsis an association that was suggested in clip studies by Shi et al[15].
Pehlivanov et al[6] showed a significant correlation between maximum muscle thickness and pressure amplitude during esophageal bolus transport, which we now may interpret as a correlation between LLS and closure pressure as was shown explicitly by Nicosia et al[1]. These results support the physiological explanation of longitudinal muscle function discussed above, since a higher degree of LLS would imply a higher concentration of circular muscle fibers and, potentially, a higher closure pressure (equation 1, Figure 4). Pehlivanov et al[23] went on to show that this correlation weakens in patients with nutcracker esophagus and diffuse esophageal spasm, suggesting that pathology of circular and longitudinal muscle during bolus transport may be intertwined. Interestingly, Balaban et al[24] demonstrated a correlation in thickening of the esophageal muscularis propria sustained for a minute and chest pain, in the absence of peristalsis and circular muscle contraction. In the absence of a bolus, an increase in muscle thickness implies an increase in muscle cross sectional area, so we may conclude that the recorded chest pain was associated with sustained shortening of esophageal longitudinal muscle.
Using mucosal clips in the distal esophagus, Kahrilas et al[13] showed that longitudinal shortening is impaired by hiatal hernia. This result is understandable in light of the balance between longitudinal muscle stress orad, and elastic stress within the phreno-esophageal ligaments caudal, as discussed above. The mucosal clip study by Shi et al[15] suggests that transient lower esophageal relaxation (tLESR) may be associated with longitudinal shortening of the distal esophagus, and therefore that gastro-esophageal reflux may be preceded by longitudinal muscle contraction and esophageal shortening. A recent study reported by Pandolfino et al[25], with far more subjects that combine two mucosal clips with high-resolution manometry, provides convincing evidence that this is the case. The physiology and function of local longitudinal shortening in reflux, and in distinguishing normal from pathological reflux, is not yet understood.
Research within the last several years has greatly increased our understanding of longitudinal muscle function in the esophagus. In particular, we now have a reasonable explanation for why evolution has lead to the creation of a longitudinal muscle layer. Peristalsis underlies esophageal function. From a mechanical perspective, peristalsis requires force and power. From a physiological perspective, the peristaltic forces originate in the generation of muscle fiber tone, regulated and controlled in space-time by central and enteric neuromuscular interactions. Underlying luminal transport in the esophagus, transport and mixing in the gut, and regulation of transport in the sphincters, is the controlled opening and closure of localized luminal segments by circularly aligned muscle fibers. Thus the efficiency of circular muscle function underlies the efficiency of gut function. We have observed (Figure 8) that at peak closure pressure, the circular muscle layer area and thickness in the esophagus are roughly three times larger than the resting state, implying that in the absence of the longitudinal muscle layer, the circular muscle should have to be three times thicker than evolution has produced. Thus, taking into account a longitudinal muscle layer with the same thickness as the circular muscle layer, and assuming the same number density of longitudinal and circular muscle fibers, the presence of a longitudinal muscle layer implies a 33% savings in the required number of muscle fibers.
However, the savings are much greater than simply a reduction by one third in the number of required muscle fibers. By producing a local wave of longitudinal muscle contraction coordinated with circular muscle contraction, the longitudinal muscle layer generates controlled axial motions of the mucosal surface that affect the frictional and pressure stresses within the fluid lubrication layer between the mucosa and catheter, or within the mucosal folds. The consequence of these changes is to reduce by two thirds the pressure force required to close the lumen and effect peristaltic transport, and therefore the tension force by each circular muscle fiber. The major reductions in circular muscle force also imply major reductions in power required to transport the bolus, and therefore the energy required by the circular muscle fibers during peristalsis. If one assumes that axial stresses induced by longitudinal muscle contraction are, at best, comparable to the hoop stresses during peristalsis, the additional power required by longitudinal muscle is of order or less than circular muscle, and a net savings of at least one third is again obtained. Thus, the presence of the longitudinal muscle layer both reduces substantially the number of muscle fibers required for peristaltic bolus transport and the energy required by the muscles involved in the transport process. The motivation for the existence of a longitudinal muscle layer is clear.
Whereas the mechanical consequences of longitudinal muscle function in esophageal peristalsis are somewhat clarified, there is very little that is understood about the neurophysiology that controls the coordination between longitudinal and circular muscle peristalsis, or about the function and physiology of longitudinal muscle not associated with peristalsis. Furthermore, whereas there have been some tantalizing hints about the role of longitudinal muscle in pathology, very little is known, much less understood, about longitudinal muscle pathology, its role in gut dysfunction, and its relationship to diseases of the gastro-intestinal tract.
S- Editor Liu Y L- Editor Alpini GD E- Editor Ma WH
| 1. | Nicosia MA, Brasseur JG, Liu JB, Miller LS. Local longitudinal muscle shortening of the human esophagus from high-frequency ultrasonography. Am J Physiol Gastrointest Liver Physiol. 2001;281:G1022-G1033. [PubMed] |
| 2. | Dai Q, Korimilli A, Thangada VK, Chung CY, Parkman H, Brasseur J, Miller LS. Muscle shortening along the normal esophagus during swallowing. Dig Dis Sci. 2006;51:105-109. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 19] [Cited by in RCA: 18] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 3. | Ulerich R, Dai Q, Miller LS, Brasseur JG. Detailed 3-D Anatomy of the Human Gastro-Esophageal Segment. Gastroenterology. 2003;124:A259-A259. |
| 4. | Liu JB, Miller LS, Goldberg BB, Feld RI, Alexander AA, Needleman L, Castell DO, Klenn PJ, Millward CL. Transnasal US of the esophagus: preliminary morphologic and function studies. Radiology. 1992;184:721-727. [PubMed] |
| 5. | Miller LS, Liu JB, Colizzo FP, Ter H, Marzano J, Barbarevech C, Helwig K, Leung L, Goldberg BB, Hedwig K corrected to Helwig K. Correlation of high-frequency esophageal ultrasonography and manometry in the study of esophageal motility. Gastroenterology. 1995;109:832-837. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 54] [Cited by in RCA: 56] [Article Influence: 1.9] [Reference Citation Analysis (0)] |
| 6. | Pehlivanov N, Liu J, Kassab GS, Puckett JL, Mittal RK. Relationship between esophageal muscle thickness and intraluminal pressure: an ultrasonographic study. Am J Physiol Gastrointest Liver Physiol. 2001;280:G1093-G1098. [PubMed] |
| 7. | Brasseur JG, Dodds WJ. Interpretation of intraluminal manometric measurements in terms of swallowing mechanics. Dysphagia. 1991;6:100-119. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 91] [Cited by in RCA: 77] [Article Influence: 2.3] [Reference Citation Analysis (0)] |
| 8. | Li M, Brasseur JG. Nonsteady peristaltic transport in finite length tubes. J Fluid Mech. 1993;248:129-151. [DOI] [Full Text] |
| 9. | Nicosia MA, Brasseur JG. A mathematical model for estimating muscle tension in vivo during esophageal bolus transport. J Theor Biol. 2002;219:235-255. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 28] [Cited by in RCA: 29] [Article Influence: 1.3] [Reference Citation Analysis (0)] |
| 10. | Dodds WJ, Stewart ET, Hodges D, Zboralske FF. Movement of the feline esophagus associated with respiration and peristalsis. An evaluation using tantalum markers. J Clin Invest. 1973;52:1-13. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 102] [Cited by in RCA: 85] [Article Influence: 1.6] [Reference Citation Analysis (0)] |
| 11. | Lin S, Brasseur JG, Pouderoux P, Kahrilas PJ. The phrenic ampulla: distal esophagus or potential hiatal hernia? Am J Physiol. 1995;268:G320-G327. [PubMed] |
| 12. | Edmundowicz SA, Clouse RE. Shortening of the esophagus in response to swallowing. Am J Physiol. 1991;260:G512-G516. [PubMed] |
| 13. | Kahrilas PJ, Wu S, Lin S, Pouderoux P. Attenuation of esophageal shortening during peristalsis with hiatus hernia. Gastroenterology. 1995;109:1818-1825. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 79] [Cited by in RCA: 65] [Article Influence: 2.2] [Reference Citation Analysis (0)] |
| 14. | Pouderoux P, Lin S, Kahrilas PJ. Timing, propagation, coordination, and effect of esophageal shortening during peristalsis. Gastroenterology. 1997;112:1147-1154. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 93] [Cited by in RCA: 90] [Article Influence: 3.2] [Reference Citation Analysis (0)] |
| 15. | Shi G, Pandolfino JE, Joehl RJ, Brasseur JG, Kahrilas PJ. Distinct patterns of oesophageal shortening during primary peristalsis, secondary peristalsis and transient lower oesophageal sphincter relaxation. Neurogastroenterol Motil. 2002;14:505-512. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 34] [Cited by in RCA: 33] [Article Influence: 1.4] [Reference Citation Analysis (0)] |
| 16. | Thatte A, Brasseur JG. The Misuse of the Laplace Law in Measurement of Gastro-Intestinal Wall Compliance. (abstract). Bull Amer Phys Soc. 2005;50:88. |
| 17. | Sugarbaker DJ, Rattan S, Goyal RK. Mechanical and electrical activity of esophageal smooth muscle during peristalsis. Am J Physiol. 1984;246:G145-G150. [PubMed] |
| 18. | Pal A, Brasseur JG. The mechanical advantage of local longitudinal shortening on peristaltic transport. J Biomech Eng. 2002;124:94-100. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 56] [Cited by in RCA: 42] [Article Influence: 1.8] [Reference Citation Analysis (0)] |
| 19. | Mittal RK, Padda B, Bhalla V, Bhargava V, Liu J. Synchrony between circular and longitudinal muscle contractions during peristalsis in normal subjects. Am J Physiol Gastrointest Liver Physiol. 2006;290:G431-G438. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 65] [Cited by in RCA: 62] [Article Influence: 3.3] [Reference Citation Analysis (0)] |
| 20. | Ghosh SK, Kahrilas PJ, Zaki T, Pandolfino JE, Joehl RJ, Brasseur JG. The mechanical basis of impaired esophageal emptying postfundoplication. Am J Physiol Gastrointest Liver Physiol. 2005;289:G21-G35. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 33] [Cited by in RCA: 36] [Article Influence: 1.8] [Reference Citation Analysis (0)] |
| 21. | Dai Q, Liu JB, Brasseur JG, Thangada VK, Thomas B, Parkman H, Miller LS. Volume (3-dimensional) space-time reconstruction of esophageal peristaltic contraction by using simultaneous US and manometry. Gastrointest Endosc. 2003;58:913-919. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 7] [Cited by in RCA: 9] [Article Influence: 0.4] [Reference Citation Analysis (0)] |
| 22. | Yamamoto Y, Liu J, Smith TK, Mittal RK. Distension-related responses in circular and longitudinal muscle of the human esophagus: an ultrasonographic study. Am J Physiol. 1998;275:G805-G811. [PubMed] |
| 23. | Pehlivanov N, Liu J, Kassab GS, Beaumont C, Mittal RK. Relationship between esophageal muscle thickness and intraluminal pressure in patients with esophageal spasm. Am J Physiol Gastrointest Liver Physiol. 2002;282:G1016-G1023. [PubMed] |
| 24. | Balaban DH, Yamamoto Y, Liu J, Pehlivanov N, Wisniewski R, DeSilvey D, Mittal RK. Sustained esophageal contraction: a marker of esophageal chest pain identified by intraluminal ultrasonography. Gastroenterology. 1999;116:29-37. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 152] [Cited by in RCA: 137] [Article Influence: 5.3] [Reference Citation Analysis (0)] |
| 25. | Pandolfino JE, Zhang QG, Ghosh SK, Han A, Boniquit C, Kahrilas PJ. Transient lower esophageal sphincter relaxations and reflux: mechanistic analysis using concurrent fluoroscopy and high-resolution manometry. Gastroenterology. 2006;131:1725-1733. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 152] [Cited by in RCA: 141] [Article Influence: 7.4] [Reference Citation Analysis (0)] |