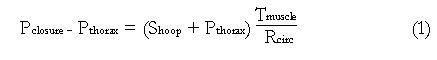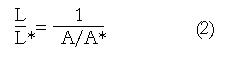Copyright
©2007 Baishideng Publishing Group Co.
World J Gastroenterol. Mar 7, 2007; 13(9): 1335-1346
Published online Mar 7, 2007. doi: 10.3748/wjg.v13.i9.1335
Published online Mar 7, 2007. doi: 10.3748/wjg.v13.i9.1335
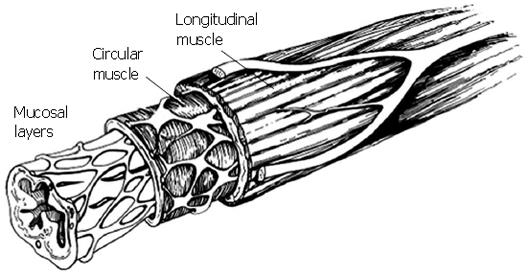
Figure 1 Schematic of esophageal cross section, showing the primary esophageal layers.
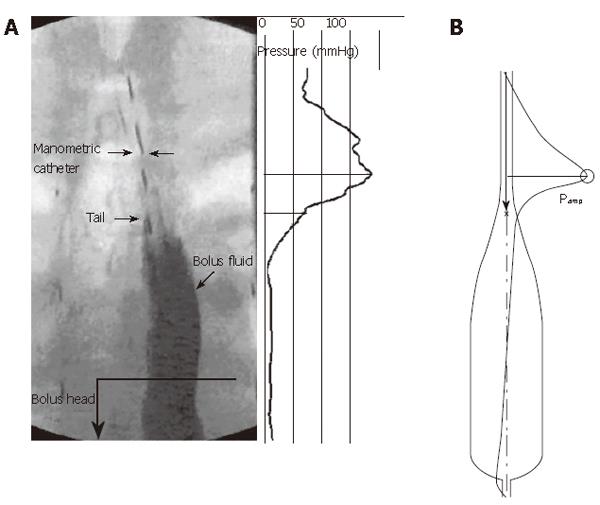
Figure 2 Frozen time image of peristaltic transport of a liquid bolus through the esophagus, with corresponding spatial variation in intraluminal pressure.
A: Fluoroscopic image and pressure distribution (relative to atmospheric) concurrent with interpolated high-resolution manometry data; B: Bolus shape and overlayed pressure distribution from a mathematical model computer simulation.
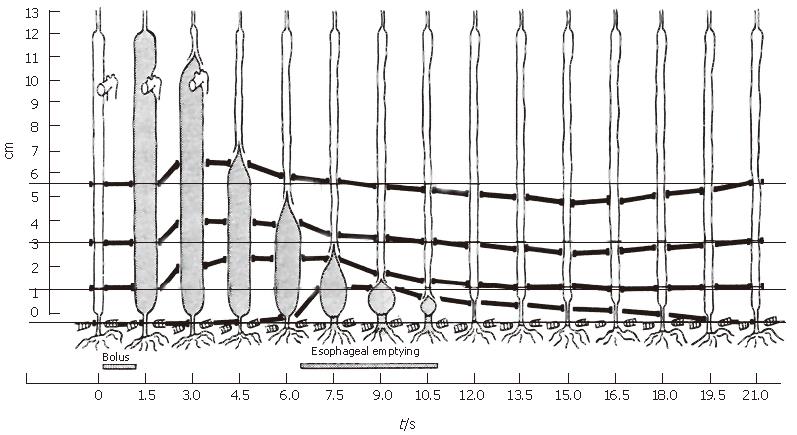
Figure 3 The classic experiment by Dodds et al[10] in which the motion of four material points in the muscle wall of the feline esophagus were recorded over time concurrently with bolus transport using fluoroscopy.
Figure 4 Schematic of the force balance across an axial segment of the muscularis propria of the esophageal wall, showing the relationship between closure pressure (Pclosure) and average hoop stress (Shoop) across the circular and longitudinal muscle layers.
Math 1 Math(A1).
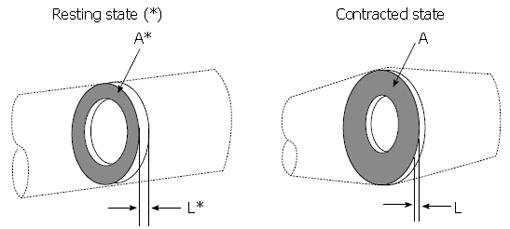
Figure 5 Application of the principle of mass conservation to quantify local longitudinal shortening from measurement of the change in cross sectional area from endoluminal ultrasound images, leading to L/L* = 1/(A/A*).
Math 2 Math(A2).
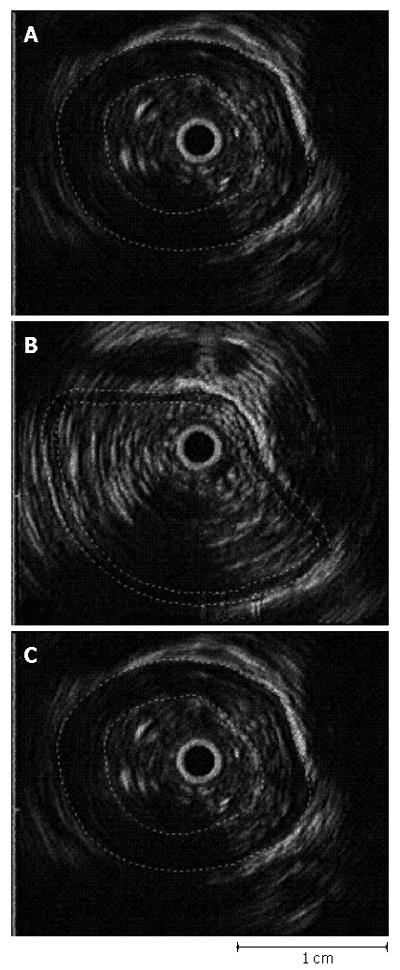
Figure 6 Example of the use of EUS with image analysis to determine the cross sectional area of the muscularis propria (A) in the resting state (*), (B) with distention at the bolus head, and (C) at peak contractile pressure.
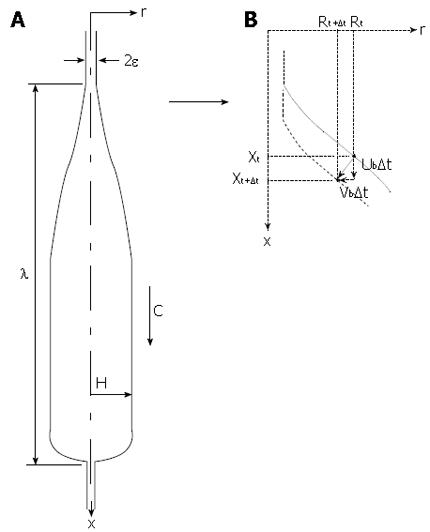
Figure 7 Schematic of essential elements in the mathematical model.
A: Bolus shape with geometrical parameters. H is the bolus head radius, λ is bolus length, ε is the thickness of the lubrication layer in the contracted zone, and c is the peristaltic wave speed; B: Specification of mucosal surface velocity in the model. Ub and Vb are the axial and radial surface velocity components, respectively, of a material element of the mucosal surface.
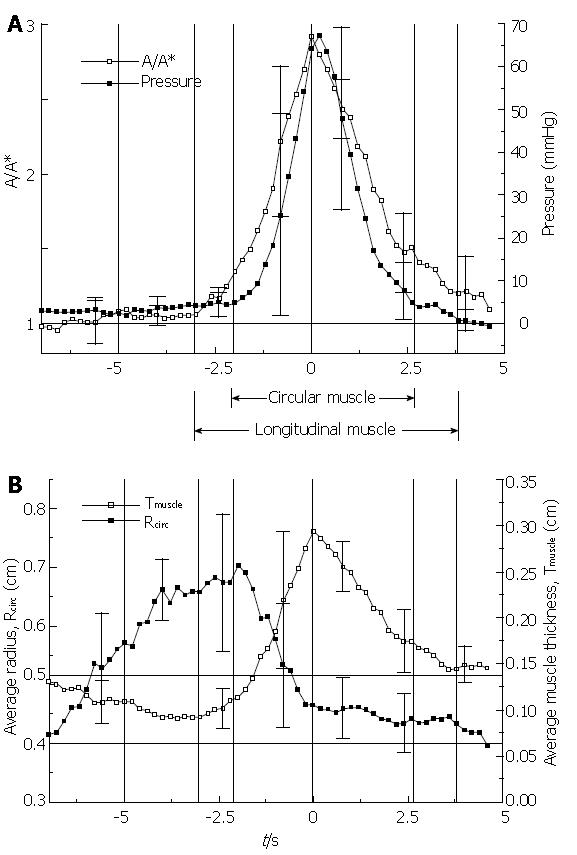
Figure 8 The primary result from Nicosia et al[1].
In (A) the inverse of local longitudinal shortening (A/A* = 1/(L/L*), see equation 2) is plotted together with circular muscle closure pressure (see equation 1) and in (B) the effective thickness of the muscularis propria is plotted together with effective lumen radius. All variables are plotted during the passage of a peristaltic wave with the transport of a 10 mL liquid bolus in the mid esophagus. Averages over four normal subjects were done referenced to the peak in LLS.
Figure 9 From Dai et al[2], local longitudinal shortening at peak intraluminal pressure during swallowing of 5 mL water bolus at different locations above the upper margin of lower esophageal sphincter high-pressure zone.
Averages of 20 normal subjects.
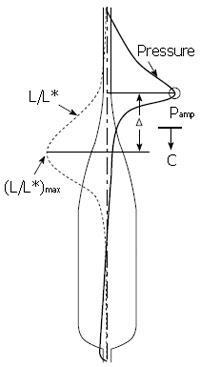
Figure 10 Schematic of the parameterization of local longitudinal shortening in the model.
The shape of the shortening parameter L/L* is fixed while maximum LLS and offset between the longitudinal and circular muscle contraction waves are varied.
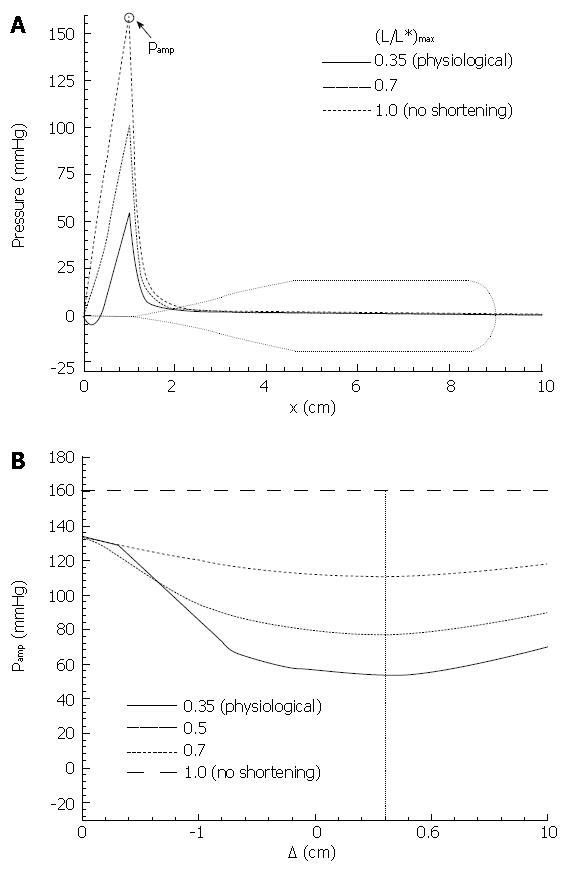
Figure 11 Primary result from Pal & Brasseur[18].
A: Mathematical model calculation of pressure during esophageal peristaltic transport with different levels of local longitudinal shortening, from the measured physiological level, to no shortening; B: Calculation of peak closure pressure as a function of separation △ between the circular muscle and longitudinal muscle contraction waves (Figure 10).
-
Citation: Brasseur JG, Nicosia MA, Pal A, Miller LS. Function of longitudinal
vs circular muscle fibers in esophageal peristalsis, deduced with mathematical modeling. World J Gastroenterol 2007; 13(9): 1335-1346 - URL: https://www.wjgnet.com/1007-9327/full/v13/i9/1335.htm
- DOI: https://dx.doi.org/10.3748/wjg.v13.i9.1335