INTRODUCTION
The understanding of functions of biological macromolecules has relied not only on the structural data but also their dynamical behavior. The early view of the proteins as relatively rigid structures has been replaced by a dynamic model. In these models conformational changes and motions play an essential role in their function. In the last 25 years, biomolecular simulations has become a powerful tool to trace atomic motions of protein and DNA molecules and yielded important insights into molecular mechanisms[1-3]. The molecular dynamics (MD) simulation is considered a pivotal methodology to access dynamical behavior of macromolecules in silico. This technique provides ultimate atomic resolution details about the dynamic properties of the system as a function of time. It offers connection between the structure and function by enabling the exploration of the conformational space and energy landscape available to protein molecules. It is not surprising that the term “computational microscope” has been accepted by the scientific community[4].
One of the first MD simulations of proteins, bovine pancreatic trypsin inhibitor (BPTI), was reported in 1977. This work should be considered as the first attempt to utilize computer simulation to observe protein motions at 9.2 picosecond (ps) time scale[5]. In 1988, eleven years later, the same protein was simulated for 210 ps using explicit solvent[6]. The latter work showed good correlation between the average structure produced by simulation and the high-resolution X-ray structure, emphasizing the importance of longer simulation time and use of explicit water molecules. Since then the dramatic increase in computational power and significant improvement in methodology made the simulation much more accurate and stable. It is now routine to run simulations from 100 ns (10-7 s) to several μs (10-6 s) where even shorter time scales (10-100 ns) can well describe local dynamics of the proteins structures. Experimental measurements show that rotation of protein side chains often occurs around 0.5 ns timescale [“Physical Biology of the Cell”, Rob Phillips, Jane Kondev and Julie Theriot (2009) and references therein]. However, since many functionally important biological events occur on timescales of many microseconds or milliseconds, including protein folding, protein-protein or protein-drug interactions, much longer time scales are needed for conformational sampling. Recently, there were a large number of efforts to extend simulations to a longer timescales by designing specialized hardware to speed up MD simulations and/or by improving the code[7-9]. The longest MD simulation published to date is a millisecond (ms) [1000 microsecond (μs)] simulation of the BPTI protein on a special-purpose supercomputer (called Anton) designed for MD simulations[10-12]. This work showed that BPTI transitioned reversibly among a small number of structurally distinct states with two states in the simulation accounting for 82% of the trajectory which agreed well with experimental data. Such behavior could not be observed at shorter (μs) timescales and thus confirms the importance of adequate simulations times.
The MD relies on the solution of the equations that describes the motion of the molecular system. In explicit, all-atom simulations, thousands to millions of individual atoms, representing, for instance, all atoms of the protein and surrounding water molecules, move in a series of short [e.g., 2 femtoseconds (fs)], discrete time steps. The MD trajectory represents the sequential set of time-evolved snapshots of atomic coordinates and generally provides data only at the level of atomic positions, velocities and single-point energies. The application of statistical thermodynamics allows to obtain macroscopic properties such as pressure, heat capacity and free energies of the system. The product is a detailed “movie” of molecular behavior over time. As a result, MD has became a tool for researches to investigate structural aspects, kinetics and thermodynamics of various macromolecule systems, including the dynamics in enzyme activity[13-15], transport of ion and small molecules[16-18], protein-protein and protein-DNA interactions [19-21], protein folding[22,23] and ligand-target interactions[24-27], just to mention a few. In general, each step in MD simulations consists of computationally intensive force calculations, followed by a less expensive integration step that advances the positions of the atoms according to classical laws of motions. Forces for each atom of the system are calculated based on the molecular mechanics equations. The functional form of such equations is shown in Figure 1. The potential energy parameters (bond lengths, vibrational energies, force constants, atomic and partial atomic charges, proper van der Waals atomic radii, etc.) are derived empirically from experimental techniques such as spectroscopy and X-ray crystallography, and also from ab initio quantum mechanical calculations. Collectively, these parameters describe the contributions of various atomic forces that govern MD and are called a ‘force field’. There are several well established force fields which are currently being used and continued to be developed. The Chemistry at HARvard Macromolecular Mechanics (CHARMM) biomolecular force field developed by Karplus et al[28,29] is widely used for the simulation of proteins and other many particle systems using CHARMM and NAMD molecular simulation programs[30]. The Assisted Model Building with Energy Refinement (AMBER), developed by the Kollman group[31], is a set of molecular mechanical force fields for the simulation of biomolecules, which was initially developed for the nucleic acids and now adopted for the simulation of a wide range of the biomolecules, including proteins. AMBER has a package of molecular simulation programs and can also be used by NAMD. There are several others that are available, including the Energy Calculation and Dynamics (ENCAD) developed by Levitt [32], the GROMOS and the hydrocarbon force fields (MM2-4)[33]. ENCAD and CROMOS force fields are available through the Groningen Machine for Chemical Simulations computational package[7]. In general, the force fields express the total force on an atom as a sum of 3 major components: bonded forces which involve interactions between small groups of atoms connected by one or two covalent bonds; van der Waals forces which include interactions between small groups of atoms in the system; and electrostatic forces which include interactions between all pairs of atoms (non-bonded pair-wise interactions) (see the functional form of AMBER equation, Figure 1). Chemical bonds and atomic charges are modeled using simple harmonic motions, and dihedral angles are modeled using a sinusoidal function that approximates the energy differences between eclipsed and staggered conformations. The non-bonded forces arise from van der Waals forces and electrostatic interactions. The non-bonded energy terms between every pair of atoms increase as the square of the number of atoms for a pairwise model (N2) and represent largest summation term in the potential energy equation. This part of the simulations is the most computationally expensive. The van der Waals forces fall quickly with the distance and in computer simulations are treated with 12/6 Lennard-Jones potentials. To reduce the cost of calculations the contributions from these forces can be controlled by the user defined cutoff distance. The very short cutoff (-4 Å) does not adequately model the properties of the system when a very long cutoff (over 20 Å) significantly increases simulation time and has been shown not to improve fidelity of the simulation over the intermediate values around 9-12 Å which are commonly used in the modern simulation[34]. The electrostatic forces fall off slowly with distance and truncation at cutoff distance introduces significant errors in the simulations. Electrostatic forces, modeled using Coulomb’s law, are typically computed using approximate methods (such as Ewald summations) that account for long-range effects with the explicit interaction of all pairs of atoms[35,36]. However, recent studies showed that use of approximation methods could affect the results of the simulations. For example, in case of the protein folding using short (9 Å) cutoff distances could shift the balance between hydrophobic and hydrophilic interactions leading to stabilization of the more compact structures[37]. Moreover, the neglect to include long-range component of the Lennard-Jones interactions and the lack of highly accurate treatment of the long-range electrostatics could result in artifacts during the folding pathways. In contrary, the free energy of the protein folding and structural properties of the folded protein are relatively unaffected by these approximations[37]. The level of the approximations used in MD simulations should depend in part on the goal and questions that these calculations are planned to address.
Figure 1 An example of the equation used to calculate atomic forces.
The equation describes potential energy in the Assisted Model Building with Energy Refinement force field. The first summation term represents the energy between the covalently bonded atoms. Summing of the angles, second term, represents the energy due to the angle geometry. Third term represents the energy of the torsion angles. Forth term accounts for the energy of the non-bonded interactions between all pairs of atom. This term can be decomposed into van der Waals and electrostatic energies. The subscript zero represents equilibrium values. The energy terms are parameterized to fit experimental (for example, spectroscopic) data and/or quantum-mechanical calculations.
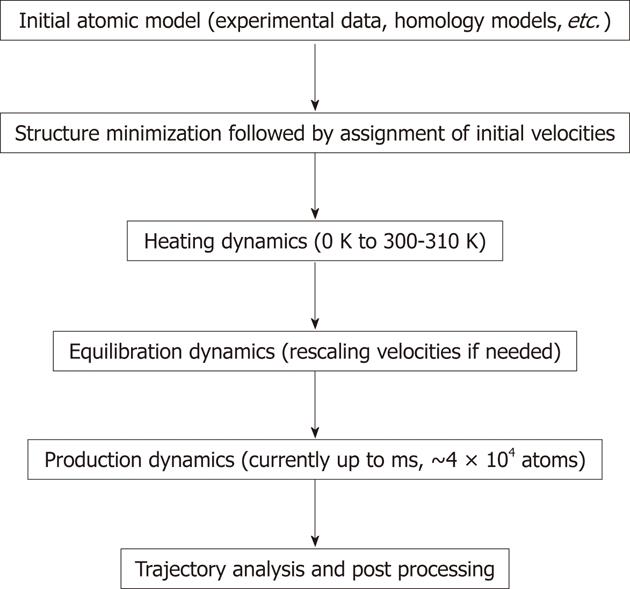
The common protocol for performing MD simulations consists of a number of steps and is shown in Figure 2. In simulations of biomolecules, an X-ray crystal structure or an nuclear magnetic resonance (NMR) structure is first obtained from the Brookhaven Protein Databank to be commonly used as the initial structure. It is also possible to use a theoretical structure developed by homology modeling (also known as comparative modeling) or extended protein sequence if the researcher desires to investigate protein folding. Prior to starting MD simulation, it is recommended to perform energy minimization of the structure to remove any strong van der Waals interactions which might exist in the initial structure. These unwanted interactions can lead to local structural distortion resulting in an unstable simulation. At this point, explicit water molecules are added to solvate the system. Another energy minimization with the macromolecule fixed should follow the solvation step to allow the added water molecules to readjust around the protein molecule. At this point, the initial velocities at a low temperature are assigned to each atom of the system and Newton’s equations of motion are integrated to propagate the system in time. In explicit solvent simulation, the protein position is fixed initially to allow equilibration of water molecules. Once that is done, the constraints on the protein can be removed and the whole system (macromolecule system and waters) can evolve in time. At the beginning of simulations velocities are assigned at low temperature and simulation proceeds via heating phase. Periodically, if needed, new velocities are assigned at a slightly higher temperature and the simulation is allowed to continue. This is repeated until the desired temperature is reached (commonly around 300-310 K). Once the desired temperature is reached, the equilibration simulation of the system continues and properties such as structure, pressure, temperature and energy are monitored. The purpose of equilibration dynamics is to run the simulation until these properties become stable with respect to time. If the temperature increases or decreases significantly, the velocities can be scaled such that the temperature returns to near its desired value. The final step of the simulation is to run the simulation in “production” phase for the desired time length. This can be from several to 106 ns. The MD trajectories from the production dynamics can be analyzed and post-processed to obtain conformational dynamics, thermodynamic parameters and free energy values for the system of interest. There are many modifications of the procedure described above using different protocols to control the temperature and generate MD trajectories. The additional details on MD procedures and theory can be found elsewhere[38-40]. The new methods such as replica-exchange MD (REMD) have been developed and employed for the simulation of macromolecules[41]. A series of replicas are run in parallel at temperatures ranging from a desired temperature to a high temperature at which the replica can easily overcome small energy barriers[42]. The REMD approach can overcome the multiple-minima problem known to trap structures in the local conformational minimum by exchanging non-interacting replicas of the system at several temperatures.
Figure 2 General steps used in molecular dynamics simulations.
During the simulations molecular focus on each atom are calculated based on the equation shown in Figure 1. During dynamics calculations (heating, equilibration and production) the positions of atoms are moved according to Newton’s law of motion. The simulation time is advanced, and the process is repeated numerous times to generate molecular dynamics rajectory. The longest trajectory is generated during the production run.
The vast increase in the number of MD papers published in the last 10 years, including publications in those highly respected journals such as Nature and Science, is a clear evidence that MD simulations become a widely accepted tool for investigation of conformational features for biological macromolecules. The number of publications using MD is now in tens of thousands. For example, using “molecular dynamics” and “proteins” as topic words to search ISI “web of science” (http://apps.webofknowledge.com/) yielded almost 4000 papers in 2011 vs about 1200 articles in 2001. Therefore, it is impossible for such a short review to adequately describe all major work done using MD simulations. Here we chose to describe a small number of specific examples to illustrate the use of the MD simulations to obtain functionally relevant information.
MD AND PROTEIN FOLDING
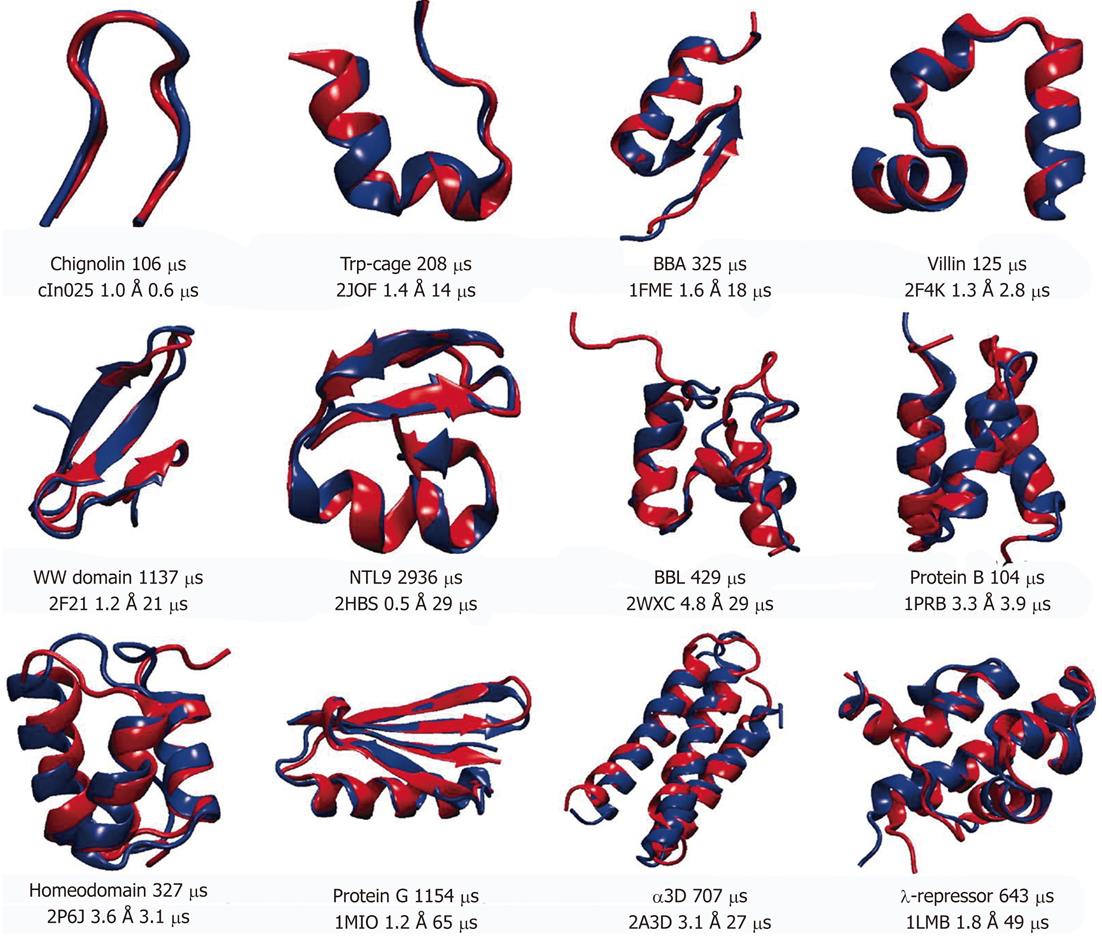
Understanding the protein folding or how the polypeptide chain is able to fold to its native conformation is essential to the description of the function of the protein. It is well established that misfolding is present in a variety of diseases[43]. One of the key aspects of the protein folding is the mechanisms by which the protein finds the native conformation despite enormous number of statistically possible conformations. In addition, the folding is slow on the simulation time scale with many proteins taking microseconds to fold. So far only small sized proteins (10 to 80 amino acid residues), with no disulfide bonds or prostatic groups, have been successfully folded to its native conformation. The small sizes and rather short folding times of such proteins make them good candidates for MD simulation using all-atom models in explicit solvent since the native conformation of these proteins is determined solely by the protein amino acid sequence[44]. The recent work from the DE Shaw group[45] summarized the simulations of 12 proteins which represent three major structural classes (α-helical, β-sheet and mixed α/β). All simulations started from extended conformations to avoid bias toward the native state. In that work total of approximately 8 ms of MD simulations were collected. Figure 3 shows the representative structures of those 12 proteins. For each protein MD folded structure is shown in blue and superimposed on the experimental determined structure. For most of the structures (8 out of 12) the root mean square deviations of Cα atoms (Cα-RMSDs) between the two structures, which includes flexible tails residues, were below 2 Å, indicating an excellent agreement between experiment and simulation. To confirm the finding of this work, simulations were performed near the melting temperature, at which both unfolding and folding could be observed repeatedly bringing total to 10 unfolding and 10 folding events for each protein[45]. The authors collected about 400 folding and unfolding events for a total of 8 ms of simulation. The proteins exhibiting larger RMSD values (BBL, protein B, homeodemain and α3D) all contain 3 α-helices. It is possible to suggest that this could indicate minor imperfections of the force-field, however, it is also possible to assume that the experimentally determined conformations for these proteins depend on experimental conditions[46,47]. Deviations between the MD and experimental data might represent differences between the protein’s structure at the simulated temperature and the lower temperatures used for experimental structure determination. Based on the MD simulations reported by Lindorff-Larsen et al[45], the authors were able to propose general principles that underline protein folding. They concluded that the pathway toward the native conformation occurs via formation of the key long-range contacts at the early stages of the folding. These contacts support secondary structure elements which are only formed in the unfolded state. Nine out of 11 proteins simulated in that work share more than 60% of the native contacts formed at any given time during the folding process. The formation of number of structural elements was observed in the similar order, suggesting a common folding pathway for the proteins studied. It is reasonable to propose that heterogeneous folding process for various proteins share a large fraction of structural features and could belong to the same folding “route”. The examination of the thermodynamics and kinetics of the folding process showed the absence of a distinct free-energy barrier for folding and the analysis yielded multiple barriers along the folding path which were less than 4.5 kBT. Under experimental conditions corresponding to those used in above simulations folding of the protein was also not determined by single, well-defined free-energy barrier.
Figure 3 Representative structures of 12 proteins used in molecular dynamics simulation studies[42].
Experimentally determined structures are shown in red and superimposed onto the structures obtained from molecular dynamics simulations (shown in blue). Protein Databank (PDB) entry, root mean square deviations of Cα atoms between two structures and simulation times (total and needed for folding) are displayed for each protein under the superimposed structures. For Protein G the PDB entry was used for the closest homolog, since the structure for the simulated sequence has not been solved experimentally. Reproduced with permission (Copyright 2011, Science publishing group).
Recently, an all-atom MD simulations in explicit solvent, were used to describe the folding path of the 80 amino acid λ-HG mutant of λ-repressor fragment[48]. Using the temperature-dependent MD runs the authors showed that the folding of the λ-repressor is not a two-state process as suggested before. In addition, the authors proposed possible mutation sites which could lead to a fast -folding mutant.
The results described above demonstrated that the current molecule mechanics force fields and simulations protocols are accurate and reliable to make long-time scale MD simulations as a powerful tool for characterizing large conformational changes in proteins.
MD AND DRUG DISCOVERY
For the past 20 years drug discovery has already heavily relying on the computational methods. It is reasonable to predict that computational methods, such as MD simulation, will further advance drug-optimization and enhance our ability to select and design better molecules for the interaction with specific protein targets. It is well established that molecular recognition and drug binding are a very dynamic process. In solution, when a small molecule approaches a target, it deals with the macromolecule in constant motions. Given that the static models produced by X-Ray crystallography and time-averaged structures by NMR tell little about protein dynamics, MD simulation can provide the dynamic picture of the interaction between the small molecule (such as a drug) and the target molecule. Upon binding, the ligand molecule may further induce conformational changes that are not typically sampled when the ligand is absent[49]. There are a number of examples in which binding pathways were successfully reproduced using MD simulations. The complete reconstruction of the binding process of the benzamidine molecule (a known inhibitor of serine proteases) to trypsin was achieved using 495 MD simulations of 100 ns each[50]. Out of 495 trajectories, 187 (37% of total) produced binding events with RMSD less than 2 Å from the crystallographic pose. The obtained binding paths revealed two metastable intermediate states (S2 and S3, Figure 4). The simulation showed that the inhibitor rolls on the surface of the protein prior to entry into the binding pocket (S3 to S4 transition, Figure 4). Using MD simulations the authors estimated the standard free energy of binding which was within 1 kcal/mol from the experimental value. Reconstruction of the protein-ligand binding process and identification of the transition states suggest that mutations to the transition-state residues may alter the binding kinetics of the inhibitor. Simulations of the binding of several β-blockers to two β-adrenergic receptors (G-protein-coupled receptor modulators, which constitute one-third of all marketed drugs) showed the atomic details of this pharmaceutically critical process in which drug molecules spontaneously bind to the G-protein-coupled receptors to achieve final poses matching those determined crystallographically[51]. The MD revealed dehydration of the ligand and receptor along the binding pathway that represents unexpected kinetic barrier to binding. Such work suggested how receptor/ligand dehydration, known to be a major factor for ligand affinity, might be modulated to affect drug binding kinetics. MD simulation can also be used to determine relative binding free energies between the drug candidate and target protein using Poisson-Boltzmann surface area methods[52,53].
Figure 4 Five different metastable states (S0 to S4) identified for the benzamidine-trypsin complex[47].
The relative free energy between the unbound S0 and the bound S4 states is -6 kcal/mol. The most probable transition to the bound state S4 is from S3, since the barrier between two states is just 1.5 kcal/mol. In states S1 and S2, benzamidine is stabilized by π-π stacking interactions with Y151 and Y39 side chains. In S3, a hydrogen bond may be formed between the NH2 groups of benzamidine (only heavy atoms shown for clarity) and Q175 side chain, or by a cation-π interaction between the Q175 side chain and the benzamidine’s benzene ring. Reproduced with permission (Copyright 2011, PNAS).
Besides identification of pathways and kinetics of binding, MD simulation can be used to obtain the structure of the target using folding simulations, especially in cases where the structure of the target can not be obtained experimentally. Alternatively, simulation may be used to prepare homology models.
FUTURE DIRECTIONS
Since the millisecond barrier has been broken in MD, it is more than likely that we will be able to make testable predications about the key molecular processes at the atomic levels. Based on the current progress of all-atom MD simulations, a dramatic increase in the length of the generated trajectories should be expected in the nearest future. Parallel to the increase in the timescales accessible to the simulations, there has also been a growth in the size of the systems that can be studied. Much larger systems than those mentioned above have been already tested using MD simulations. These systems are comprised of several million atoms, such as bacterial ribosomes and viruses. In recent studies explicit solvent MD simulations showed essential conformational motions in the ribosome needed for the binding of aminoacyl-tRNA[54]. Such a system consists of 3.2 million atoms. This work showed that conformational motions of the 3’-CCA end of aminoacyl-tRNA resists simple accommodation (single lock-step mechanism), leading to a multistep accommodation process. The proposed mechanism and observed interaction pathways help to interpret large number of biochemical data and demonstrate that conformational changes during translation occur through a trial-and-error process, rather than in concerted lock-step motions. The 1 million atoms simulation of satellite tobacco mosaic virus (STMV) showed that the empty STMV capsid is not stable, thus explaining the failure of experimental efforts to prepare such empty capsids[55].
Although the conformational changes in the smaller system can be well described using MD simulations, the larger systems (5 millions of atoms or more) still pose many challenges. First, the biologically relevant timescales tend to increase as the system size increases. Second, the high-resolution structures are only available for relatively few very large macromolecule complexes[56]. The computational power to carry out simulation increases can be related to the Moore’s law. This law describes how the performance of processors has been increasing exponentially over the last 50 years by doubling approximately every 2 years. Based on the application of the Moore’s law to biological systems and without taking into account the design of special hardware architecture for MD, it has been proposed that for every 10-15 years in the past there was an increase of about three orders of magnitude in the timescale and about one and half orders of magnitude in the system size used by MD simulations[57] . Continuation of Moor’s law suggests that processor computational power may increase by 1000 fold in the next 10-15 years. In addition to enhanced processor integration, software and hardware advances will yield further increases. For example, recent application of the Graphic Processing Units (GPUs), together with the development of the general purpose GPU programming model called NVIDIA’s Compute Device Architecture, can significantly increase simulation times at fraction of CPU’s cost and energy consumption. GPUs have been an integral part of personal computers for decades and their development and low cost has been strongly influenced by the entertainment industry. It has recently been shown that GPUs, due to their unique multiprocessor architecture, can greatly outperform their CPU equivalents. MD simulations can take advantage of GPU acceleration and achieve performance levels up to hundred times better than a single CPU core[58,59]. Based on the time frames obtained in the benzamidine binding studies, nowadays it is possible to reconstruct those binding pathways of 5 to 10 ligands per week on a moderately sized cluster of 32-64 GPUs[50].
It can be expected that within next 20-25 years it will be possible to simulate all-atom dynamics of a small bacterium and describe the complete set of processes within[25]. Such simulations can be probably performed for only few milliseconds or even less and would not provide much information due to large timescales needed for diffusions of macromolecules in bacterial processes. However, simulation of the part of a cell or fundamental pathways in molecular biology, such as protein synthesis, would be possible on the several seconds time-scales in the nearest future. It is obvious that macromolecule-macromolecule interactions are essential for biological processes. One major task in MD simulations is to carry out large-scale simulations of protein-protein and protein-DNA interactions. MD simulations will address the binding pathways between the macromolecules and how the ligand binding sites created, at the interface or at allosteric sites? Simulations can be expected for very large complexes such as the nuclear pore. Based on generated trajectories from such simulations it will be possible to observe passage of the delivery protein as it transits through a nuclear pore. In addition, MD will impose significant impact on the proteomics since the protein folding will be possible for larger proteins. Based on the current state of the MD simulations extrapolation suggests that folding of the 300 residues protein (over 10 ms simulation of approximately 100 000 atoms) will be possible within 10 years. Folding of the larger proteins, consisting of multiple subunits and over 1000 residues, will be still challenging and likely be achievable within 25 years[25]. Significant improvement of the time-scales might come from omitting some motions in MD simulations. It might be possible to adequately sample conformational space without resolving all fast motions, thus reducing the computational power needed for the simulation of the particular system.
With constant gains in both computer power and algorithm design, MD simulation is expected to play an increasingly important role in the modern science from investigating the local motions in the biological macromolecules to the development of novel pharmacological therapeutics. This methodology has emerged as an integral part of molecular biology studies, providing a fundamental and reliable tool for experimentalists.
Peer reviewer: Line Pedersen, PhD, Centre of Inflammation and Metabolism, Rigshospitalet, Faculty of Health Science, Copenhagen University, Blegdamsvej 9, 2100 København, Denmark
S- Editor Zhai HH L- Editor A E- Editor Xiong L