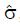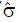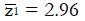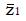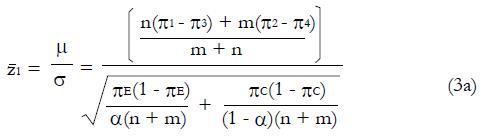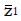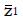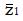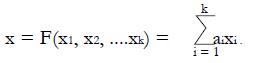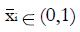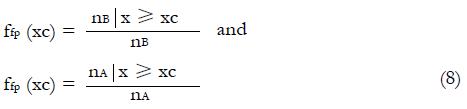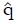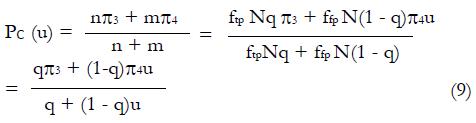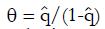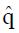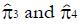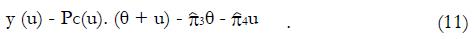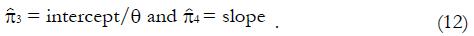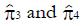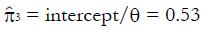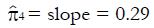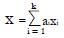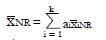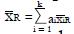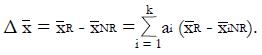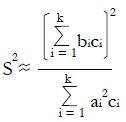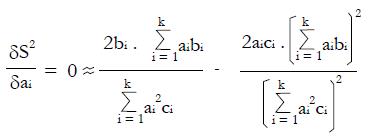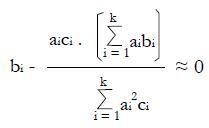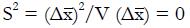Choosing inclusion criteria that minimize the time and cost of clinical trials

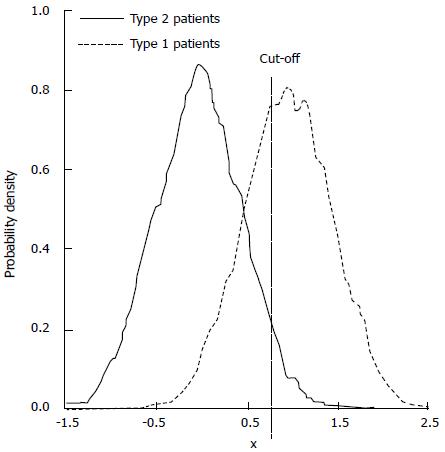
Figure 1 Separation of patient response phenotypes to a tested treatment according to an aggregate predictive variable, x. The fraction of type 1 responders to the right of the cutoff is the true positive fraction. The fraction of type 2 non-responders to the right of the cutoff is the false positive fraction. In this general example the units of x are arbitrary.

Math 10 Math(A1).

Math 11 Math(A1).

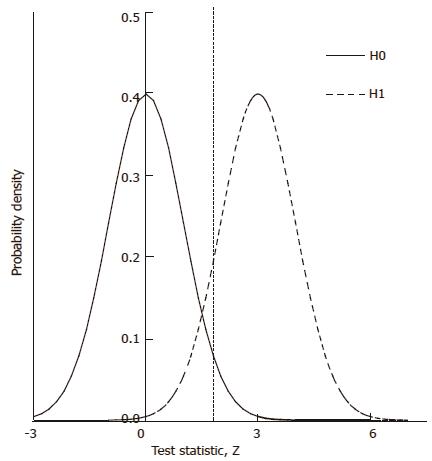
Figure 2 Calculation of power from probability density distributions for the null hypothesis (H0) and for an alternative hypothesis (H1). The dashed line shows critical value for significance (1.96 for two-tailed P < 0.05). The area under the thick curve to the right of the critical value is the statistical power of the test of H0.

Math 12 Math(A1).

Math 13 Math(A1).

Math 14 Math(A1).

Math 15 Math(A1).

Math 16 Math(A1).

Math 17 Math(A1).

Math 18 Math(A1).

Math 19 Math(A1).

Math 20 Math(A1).

Math 21 Math(A1).

Math 22 Math(A1).

Math 23 Math(A1).

Figure 3 A sample receiver operating characteristic curve for a hypothetical screening test. In this example type 1 patients had screening scores, x, with a mean of 5.5 and a standard deviation of 1; type 2 patients had screening scores, x, with a mean of 4 and a standard deviation of 1. As the cutoff value xc is swept from 1.0 toward zero, a family of true positive and false positive fractions is created to generate the receiver operating characteristic (ROC) curve.

Figure 4 Numbers of patients screened and enrolled in a model study of heterogeneous responders having a statistically significant positive result. For this model the proportion of type 1, good responders q = 0.2, the response probability for type 1 patients, π₁ = 1.0, the response probability for type 2, poor responders, π₂ = 0. The response probabilities for both phenotypes to the control treatment, π₃ and π₄ both equal 0.2. The mean value of the z statistic for the alternative hypothesis is 2.96 (84% power for the trial). The proportion of patients, α, assigned to the experimental group is 0.5.

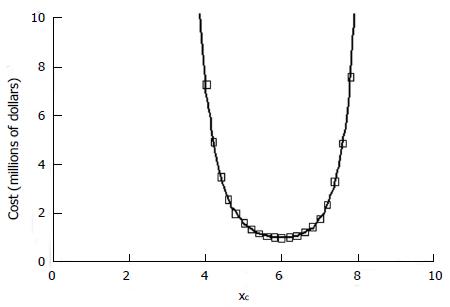
Figure 5 Cost estimates in a model study of heterogeneous responders. Cost constants in thousands of dollars are as follows: screening cost per case c₁ = 1, treatment cost c₂ = 10, opportunity cost c₃ = 100/yr, case rate r = 50/yr, follow up time t =1 yr. Other details as in Figure 4.

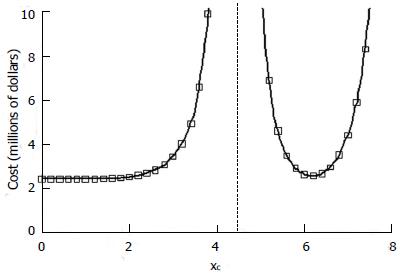
Figure 6 Cost estimates in a scenario with good responsiveness to the control treatment in patients who are non-responsive to the experimental treatment. π₁ = 1.0, π₂ = 0, π₃ = π₄ = 0.4. Other details as in Figure 5. Dashed line divides the x-domain into regions of a significant negative effect (to the left) vs a significant positive effect (right). Near x_c = 4.4 the cost of disproving the null hypothesis when it is exactly true becomes infinite.

Math 24 Math(A1).

Math 25 Math(A1).

Math 26 Math(A1).

Math 27 Math(A1).

Math 28 Math(A1).

Math 29 Math(A1).

Math 30 Math(A1).

Math 31 Math(A1).

Math 32 Math(A1).

Math 33 Math(A1).

Math 34 Math(A1).

Math 35 Math(A1).

Math 36 Math(A1).

Math 37 Math(A1).

Math 38 Math(A1).

Figure 7 Fraction of patients. A: Separation of observed responders and non-responders to the experimental treatment along the x-domain in this reconstructed preliminary study. The fraction of patients with each x-value is show on the vertical axis. Patients with x-scores over 60% have a much greater likelihood of responding; B: ROC curve for the screening procedure.

Math 39 Math(A1).

Math 40 Math(A1).

Math 41 Math(A1).

Figure 8 Regression analysis on the last two columns of Table 3. A plot of the hybrid variable, y = pC(u)(π + u), vs u can be used to evaluate model parameters π₃ and π₄. The slope of the regression line is π₄, and the intercept divided by π is π₃.

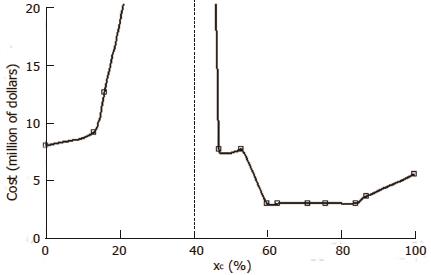
Figure 9 Cost estimates in a realistic test data set for targeted drug therapy of lung cancer, presented in Tables 2 and 3. Cost constants in thousands of dollars are as follows: screening cost per case c1 = 1, treatment cost c₂ = 10, opportunity cost c₃ = 100/year, case rate r = 50/year, follow up time t =1 year. Cost to the right of the dashed vertical asymptote are for a significant positive result (experimental treatment better than control). Costs to the left of the dashed vertical asymptote are for a significant negative result (experimental treatment worse than control).

Math 42 Math(A1).

Math 43 Math(A1).

Math 44 Math(A1).

Math 45 Math(A1).

Math 46 Math(A1).

Math 47 Math(A1).

Math 48 Math(A1).

Math 49 Math(A1).

Math 50 Math(A1).

Math 51 Math(A1).

Math 52 Math(A1).

Math 53 Math(A1).

Math 54 Math(A1).

Math 55 Math(A1).